Методы принятия решений: метод анализа иерархии и метод А.Б.Хуторецкого

декомпозицию проблемы на более простые составляющие и численную обработку суждений ЛПР с помощью метода парных сравнений.  

3.1  МАТРИЦА СРАВНЕНИЙ, ОСНОВНЫЕ ФОРМУЛЫ

Для определения весов дуг, выходящих из элемента второго или третьего уровня иерархии делаются попарные сравнения важности альтернатив относительно каждого из критериев или критериев относительно цели в качественной (словесной) шкале. При чем каждому словесному определению ставится в соответствие число (табл.1). При сравнении альтернатив, критериев ЛПР (эксперт: в данном случае им являюсь я) выражает свое мнение, используя одно из приведенных в табл.1 определений.

Таблица 1

Шкала относительной важности

Используя табл.1 я оцениваю альтернативы по первому критерию – престиж компании и данные заношу в табл.2

Таблица 2

Матрица сравнений

Матрица соответствует следующим предпочтениям ЛПР: альтернатива 1 (БСК) умеренно превосходит по важности альтернативу 2 (ЗБСМ) – оценка 5, и умеренно превосходит альтернативу 3 (Труд) – оценка 7.  Альтернатива 2 (ЗБСМ) слабо превосходит альтернативу 3 (Труд) – оценка 4.

Остальные клетки матрицы заполняются из соображений:

a_ij = 1  (1)

a_ji = 1/ a_ij   (2)

i, j = 1,n (n – количество объектов сравнения)

Полученная матрица является состоятельной, потому что выполняются указанные два свойства.

В алгоритме программ  используется понятие собственное число матрицы. Пусть Аn – квадратная матрица, вектор Х ≠ 0  называется собственным вектором An, если существует число l такое, что выполняется следующее уравнение:

Ах = l maxХ

Число l называется собственным (характеристическим) числом матрицы А с соответствующим вектору Х. из сказанного следует, что для квадратичной матрицы n-го порядка имеет место:

а11х1 + а12х2 + …+ а1nхn	=	lх1
a21х1 + а22х2 + …+ а2nхn		lх2
………………………...		….
an1х1 + аn2х2 + …+ аnnхn		lхn

(3)

Таким образом, элементы матрицы х (которые есть вектор-столбец) соответствует системе линейных уравнений:

а11х1 + а12х2 + …+ а1nхn = lх1

a21х1 + а22х2 + …+ а2nхn  = lх2

………………………............

an1х1 + аn2х2 + …+ аnnхn = lхn

(4)

Перенося члены из правой части в левую, получим:

(а11– l)х1 + а12х2 + …+ а1nхn = lх1

а21х1 + (а22– l)х2 + …+ а2nхn  = lх2

………………………............

an1х1 + аn2х2 + …+ (аnn– l)хn = lхn

(5)

Полученная система – это система из n-линейных, однородных уравнений. Она имеет ненулевое решение, если ее главный определитель равняется нулю.

Можно записать следующее:

а11– l  а12  …а1n	=	0
а21  а22 – l …а2n
…………….......
an1  аn2 … аnn – l

(6)
         Разлагая этот определитель известными нам методами, получим многочлен n-ой степени относительно переменной l. Этот многочлен называется характеристическим многочленом матрицы А, а уравнение (6) – характеристическим уравнением матрицы А.

det (A – lmax ) = 0

В нашем случае определитель будет выглядеть следующим образом:

1– l	5	7	= 0
1/5	1– l	4
1/7	1/4	1– l

Разложим матрицу, используя алгебраические дополнения. Алгебраическое дополнение D_ij элемента а_ij – число, полученное от умножения (-1)^i+j на минор М_ij. 

А = а_i1D_i1 + а_i2D_i2 +…+ а_inD_in – по строке

А = а_1jD_1j + а_2jD_2j +…+ а_njD_nj – по столбцу

Разложим по 1 строке:

(1– l)*(-1)1+1	1– l	4	+ 5*(-1)1+2	1/5	4	+7*(-1)1+3	1/5	1– l
	1/4	1– l		1/7	1– l		1/7	1/4

Þ пусть t = 1– l, тогда имеем

t (t² – 1) – 5(1/5t – 4/7) + 7(1/20 – t/7) = t³ – t – t +20/7 +7/20 – t = t³ – 3t +2,95

В результате, получим характеристическое уравнение: t³ – 3t +2,95

Для того, чтобы найти t, воспользуемся компьютерной программой Microsoft Excel. В первый столбик введем значение t (от -3 до -2 с интервалом 0,1), во второй столбик внесем формулу: =СТЕПЕНЬ(A2;3)-3*A2+2,95. Получим  какие-то значения.  Затем посмотрим, при каких значениях t, решение уравнения перескакивает с отрицательного значения на положительное. В данном случае это с  -2,1 на -2. Следовательно, в этом интервале находится значение t. (рис.4)

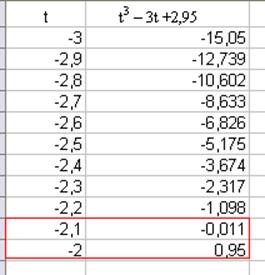
Рис.4

Для уточнения значения t проведем такую же процедуру, только теперь возьмем интервал от -2,1 до -2 с интервалом 0,001. В результате получим,    t = -2,098 (рис.5)

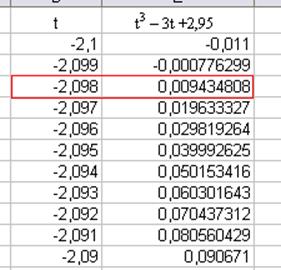
Рис. 5

Отсюда l = 1 – (-2,098) = 3,098

3.2 ИНДЕКС СОГЛАСОВАННОСТИ

Is =	lmax – n
	n – 1

Где n – размерность матрицы.

Если Is £ 0,1, то согласованность мнений эксперта на приемлемом уровне.

Если Is >0,1 – мнения эксперта несогласованны.

Признавая, что человеческие суждения находятся в постоянном процессе изменения и эволюции, настаивать не стоит на стопроцентной согласованности, так как мнения могут изменяться, после того как проблема уже решена. Но надежное решение не может быть принято без приемлемого