Метод золотого сечения. Решение дискретной задачи о выборе оптимальной траектории методами динамического программирования

Содержание

1.  Метод золотого сечения…………………………………………….2

2.  Практическая часть………………………………………………….3

2.1  Решение транспортной задачи………………………………....3

2.2  Линейное и целочисленное программирование…………………....7

2.3  Нелинейное программирование……………………………………12

2.4  Динамическое программирование. Матричные игры…………….16

3.  Список используемой литературы………………………………...18

Метод золотого сечения

      Золотым сечением отрезка называется деление его на две неравные части так, что отношение длины всего отрезка к длине большей части равно отношению длины большей части к длине меньшей части отрезка. Рассмотрим отрезок единичной длины  и две точки x и  xна нем, каждая из которых делит отрезок в отношении золотого сечения.

      Тогд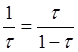а  , откуда  и положительное значение  . Величина 1-.

     Таким образом, в методе золотого сечения координаты точек экстремума на единичном интервале определяются следующим образом:  x; x. Если F(х) задается на априорном интервале [a,b] то точки эксперимента вычисляются по формулам  x= a+(b- a);  x= a+(b- a) и равно отстоят от концов отрезка. В точках эксперимента вычисляется значение функции F(x).

     Точки эксперимента на любой итерации равноудалены от границ интервала, и на каждом следующем шаге процедуры поиска должно вычисляться только одно значение функции в получаемой точке. После каждого шага текущий интервал сокращается в  раз. После проведения N испытаний апостериорный интервал неопределенности определяется выражением . Поиск заканчивается, когда длина интервала неопределенности становится соизмеримой с точностью решения задачи. Анализ метода Фибоначчи и метода золотого сечения показывает, что, начиная с некоторого числа значения экспериментов N, 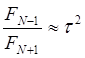, следовательно, точки испытаний на первом шаге практически одинаковы в обоих методах. Так, при N = 5 отношение 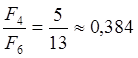, а =0,382.

Решение транспортной задачи

Вариант № 9

1. Математическая постановка транспортной задачи

Пусть имеется 4 пункта производства некоторого однородного продукта (например, угля) и 5 пунктов его потребления. Известны запасы А продукта в каждом пункте-поставщике i=1…4, спрос В в каждом пункте-потребителе j=1…5 и расходы С на перевозку единицы продукции из пункта i в пункт j. Суммарный запас равен суммарному спросу. Требуется составить план перевозок продукции, при котором запасы каждого поставщика были бы вывезены, спрос каждого потребителя был бы удовлетворен и общие транспортные расходы были бы минимальными. Условие транспортной задачи дано в таблице С1.

       Для решения этой задачи будем использовать пять различных методов: метод северо-западного угла, метод минимального элемента, метод двойного предпочтения, метод потенциалов, венгерский метод.

Матрица стоимости С1

2.  Решение транспортной задачи

Метод северо-западного угла

Матрица расстановок А1

11*21+13*19+12*14+14*22+4*8+

     +6*26+10*28=1422

Метод минимального элемента

Матрица расстановок А2

11*21+13*11+12*14+13*1

     +1*22+4*8+6*26+10*28=1045

Метод двойного предпочтения

  Матрица расстановок А3                                                                        

 24*11+2*14+10*1+11*39+

      +7*25+ +13*23+3*28=1289

Метод потенциалов

       Если матрица А1 (опорный план) является оптимальной, то ей соответствует система m+n чисел U и V, удовлетворяющая условиям:

U+V=C для X>0

U+V<=C для X=0

i=1…m, j=1…n

      Числа U и V называют потенциалами соответственно поставщиков и потребителей, С – это стоимость перевозки единицы груза занятой клетки в i-й строке и j-м столбце.

      Итерации продолжать до тех пор, пока во всех незанятых клетках не будет выполняться условие U+V<=C.

    11*21+13*19+12*14+14*22+4*8+6*26+10*28=1422
     Условию С>=U+V не удовлетворяют 3 нулевые клетки.

     1 итерация

     Из клетки U1V2 взяли 13 единиц и перенесли их в клетку U3V2. Для сохранения баланса, мы из клетки U3V3 взяли 13 единиц и перетащили в клетку U1V3, после чего получили следующую таблицу:

11*21+13*11+12*14+13*1+1*22+4*8+6*26+10*28=1045                                                                                                                                                                      
Условию C>=U+V удовлетворяют все незанятые клетки.

Венгерский метод

      Нижняя строка и правый столбец – это невязки. В Q показываются все невязки по строкам и столбцам. Минимальное значение невязки показывает насколько может уменьшиться сумма невязок после первой итерации. Сущность метода заключается в том, чтобы в конечном итоге сумму невязок свести к нулю. Продолжать итерации до тех пор, пока не будет достигнута цель метода.

                      С1                                                                                           С2

      Из матрицы стоимости С2 формируем матрицу расстановок Х0. В новой матрице вместо чисел ставим нули, а свободные клетки заполняем методом северо-западного угла.

Получим:

                   Х0

         Q=(23;2;5;16)=min=2                                    

       1 итерация

       В получившейся матрице С2 ищем минимальный элемент по строкам и столбцам. Это 14 (2;3) и заменяем его на ноль. Из столбца и строки минимального элемента вычитаем это число, а к остальным элементам матрицы добавляем его. Получили новую матрицу С3:

                    С2                                                                           С3

      Из матрицы С3 формируем матрицу Х1. В новой матрице вместо чисел ставим нули, а свободные клетки заполняем методом северо-западного угла. Получим:

                        Х1

Q=(21;5;16)=min=5

      2 итерация      

      В получившейся матрице С3 ищем минимальный элемент по строкам