


2009-09-04
Лекция 2
Инвариантность канонической формы
К канонической форме записи можно прийти от любого промежуточного вида. Имея qi(х) >= qi* => -qi(x) <= -qi* (7)
Аналогично если необходимо показатель эффективности W обратить в максимум, то его также приводят к канонической форме. W(x) -> max => W(x) -> min (8).
Ограничения в канонической форме можно упростить следующим образом.
qi(х) >= qi* => -qi(x) <= -qi* (7)
qi(х) – qi*>= 0 => qii(x) >= 0 (9)
Учитывая 8 и 9, упрощенная форма записи примет вид.
W(x) -> min (max) в зависимости от условия задачи
Qii(x) >= 0 (<=0) в зависимости от того к чему устремляем целевую функцию
Задачи можно классифицировать по виду математической зависимости 1-4:
1) Если функциональные зависимости 1,2,3 являются алгебраическими или трансцендентными, то такие задачи называются статическими.
2) Если в математической модели операции зависимые и независимые переменные связанны друг с другом с помощью дифференциальных уравнений, то такие задачи называются динамическими.
3) Если функциональные зависимости 1,2,3 являются линейными, то метод их решения линейное программирование.
4) Если переменные Х все или часть изменяются дискретно, то есть принимают целочисленное значение, то такие задачи называются дискретными, а методы их решения дискретное программирование.
5) Если коэффициенты, входящие в зависимости 1,2,3 все или их часть изменяются случайным образом, то такие задачи называются стохастическими, метод решения стохастическое программирование.
А) Когда вероятностные характеристики коэффициентов известны, это задачи в условиях риска. Вероятностные характеристики – это математическое ожидание, дисперсия , и т.д.
Б) Если вероятностные характеристики коэффициентов не известны, или известны частично , то такие задачи называются стохастическими в условиях неопределенности. А метод их решения теория Игр.
6) Если хотя бы одна переменная находится в зависимостях 1-3, находится в степени выше 1, или являются нелинейными функциями, то такие задачи называются нелинейными. Метод решения нелинейное программирование.
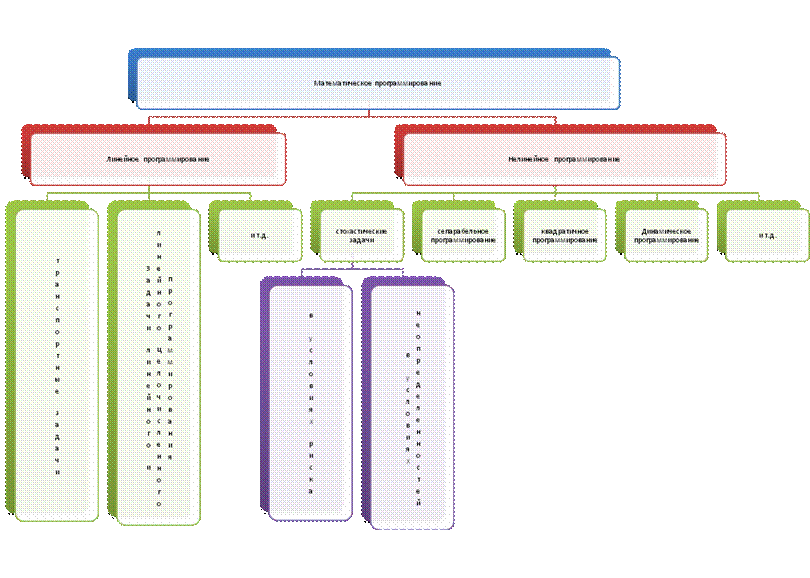
Линейное программирование включает задачи, в которых и целевая функция и ограничения линейны.
В любом операционном проекте можно выделить пять основных частей.
Этап 1 – Постановка задачи
Включает в себя выявление и определение компонентов модели, задания мер для их измерения. Задачу перед операционистами ставит руководитель. Исполнителю операционного проекта при предварительном ознакомление информацию необходимо получать от руководителя, работников управленческого аппарата, непосредственных исполнителей. В ходе ознакомления выделяются главные цели организации и возможные варианты действий при управлении, учитывая системный подход. Наиболее эффективный способ изучения системы – ее анализ. А анализ в свою очередь можно выполнять следующими способами:
А) Определить внешние потребности по отношению к рассматриваемой организации, (определение круга потребителей и их заказы)
Б) Определить способ в котором данная потребность доводится до сведения организации, информация может поступать в виде заказа который направляется в отдел сбыта. Здесь же определяется : количество сотрудников в отделе, количество счетов потребителей, количество заказов в единицу времени, распределение заказов по номенклатуре, и т.д. Степень детализации на данном этапе исследования зависит от степени существенности для постановки задачи.
В) Определить каким образом информация о потребностях регистрируется и передается в различные подразделения организации.
В общем случае с информацией, может происходить следующее:
А) Информация может быть преобразована, сжата, в результате чего появляется новый документ. Движение документа также необходимо отследить.
Б) В некоторых звеньях системы, информация может быть использована, для принятия решения, или формирования распоряжения (управляющее воздействие). В таких звеньях необходимо отследить выполнение решений.
Этап 2 – Построение математической модели (далее ММ) изучаемой системы
Этап 3 – Нахождение решения на ММ
Этап 4 – Проверка ММ и оценка полученного на ней решения
Этап 5 – Внедрение решений и контроль за их правильностью
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.