Данная модель применяется в макрологических системах, когда издержки га выполнение заказа и проверку фактического состояния запасов на складе велики, а заготовительный период и ущерб от дефицита ресурсов (невыполнения заказа) малы.
Еще одной моделью управления запасами, основанной на рассмотренных ранее моделях с фиксированным размером заказа и с фиксированной периодичностью заказа, является модель с установленной периодичностью пополнения запаса до постоянного уровня. В данной модели заказ ресурсов осуществляется через равные промежутки времени, однако в том случае, если фактический остаток ресурсов на складе снизится до уровня второго бункера, то осуществляется внеочередной заказ. Размер заказа равен разности между максимальным заказом и фактическим наличием запаса на момент заказа или между максимальным запасом и запасом в точке заказа.
Применение данной модели целесообразно при значительных изменениях в потребности ресурсов и необходимости исключить возможность их нехватки до наступления срока очередной поставки. Реализация модели требует оперативного контроля наличия запасов на складе.
В тех случаях, когда нельзя пренебрегать нестационарностью или стохастичностью отдельных параметров системы запасов, применяются более сложные модели управления запасами, для которых Q = var и τ = var.
2. СИСТЕМА РЕГУЛИРОВАНИЯ ЗАПАСОВ С ФИКСИРОВАННОЙ ПЕРИОДИЧНОСТЬЮ ЗАПАСА
Модель управления запасами с фиксированной периодичностью заказа (τ = const, Q = var) характеризуется тем, что ресурсы заказываются и поступают на склад через равные промежутки времени. Особенности данной модели отражены на рис. 7.
В момент заказа ресурсов проверяется наличие запаса на складе. Размер заказа равен разности между фиксированным необходимым запасом и его фактическим наличием
qз = Qmax – Qфакт.
Таким образом, qз является переменной величиной.
В данной модели определению подлежит уровень максимального запаса и период между двумя смежными поставками ресурсов. Максимальный уровень запаса в системе должен быть равен:
Qmax = qз + Qстр,
а величина периода между смежными заказами:
τсз = qз / λ.
Применение данной модели целесообразно при установлении регулярных сроков поставки и возможности запасать ресурсы в любом количестве. Достоинством модели является то, что при ее использовании нет необходимости в ведении регулярного (ежедневного) учета наличия запасов на складе. Это необходимо лишь в момент времени заказа ресурсов.
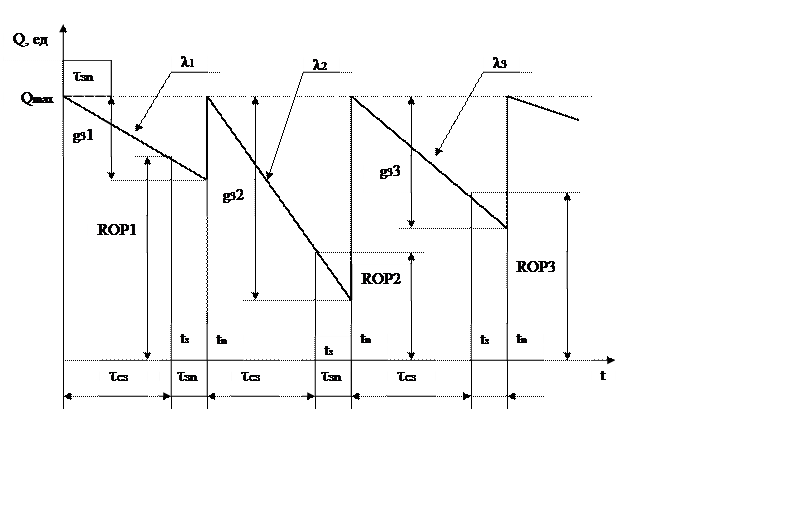
Рис. 7. Модель управления запасами с фиксированной периодичностью заказа
3. ПРАКТИЧЕСКОЕ ЗАДАНИЕ
Задача.
Определить транспортный запас в натуральном выражении, если отгружено за квартал – 200 тонн труб, а среднее время их транспортировки – 7 дней.
Решение.
Запас транспортный в натуральном выражении определяется по формуле
Зтр. н. = Зо дн ∙ Р,
где Зо дн – запас относительный в днях обеспеченности объема потребления (товарооборота); Р – объем среднесуточного потребления (отпуска) в натуральных единицах.
Найдем Р
Р = 200 тонн / 90 дней = 2,2 тонн в день.
Следовательно,
Зтр. н. = 2,2 тонны в день ∙ 7 дней = 15,4 тонны.
Транспортный запас в натуральном выражении равен 15,4 тонны.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Аникин Б. А., Тяпухин А. П. Коммерческая логистика: учеб. – М.: ТК Велби, Изд-во Проспект, 2005.
2. Логистика запасов: Практикум для студентов дневной и заочной форм обучения специальностей «Коммерция (торговое дело)» и «Маркетинг» / Сост. к. э. н., и. о. проф. О. В. Саенко. – Хабаровск: РИЦ ХГАЭП, 2001.
3. Третьяков М. М., Хальзова Н. А. Коммерческая логистика: Учеб. пособие. – Хабаровск: Изд-во Хабар. гос. техн. ун-та, 2002.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.