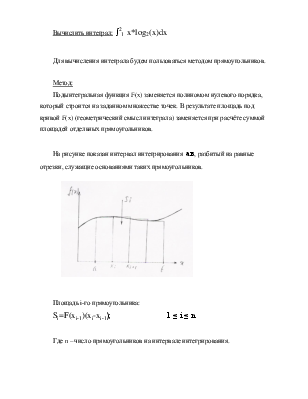

Вычислить интеграл: ∫21 x*log2(x)dx
Для вычисления интеграла будем пользоваться методом прямоугольников.
Метод:
Подынтегральная функция F(x) заменяется полиномом нулевого порядка, который строится на заданном множестве точек. В результате площадь под кривой F(x) (геометрический смысл интеграла) заменяется при расчёте суммой площадей отдельных прямоугольников.
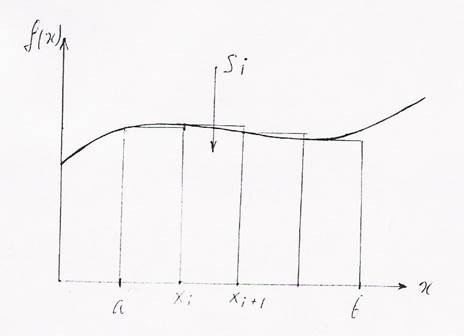 |
Площадь i-го прямоугольника:
Si=F(xi-1)(xi-xi-1); 1 ≤ i ≤ n
Где n – число прямоугольников на интервале интегрирования.
При количестве прямоугольников имеем:
∫ F(x)dx ≈ ∑ ni=1 Si
При h = (b-a)/n (где h – шаг интегрирования), численное значение интеграла:
I = h ∑ni=1 F(xi-1)
Эта формула позволяет вычислить интеграл с погрешностью, зависящей от числа отрезков разбиения n.
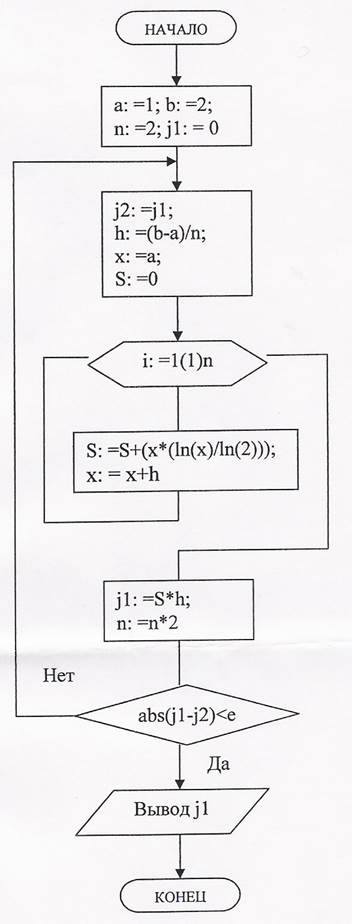
Чтобы вычисление происходило с заданной погрешностью, следует организовать итерационный процесс. Он должен начинаться с вычисления значения I.
Затем удваивают значение n и вычисляют новое численное значение интеграла.
Сравнивают разницу между двумя этими значениями интеграла с заданной погрешностью. Процесс продолжается до достижения заданной погрешности.
∫21 x*log2(x)dx;
F(x) = x*log2(x) = x*(log2(x)/log2(2)) = x*(ln(x)/ln(2))
fun – функция F(x)
niz – нижний предел интегрирования
verh – верхний предел интегрирования
n – число прямоугольников на интервале интегрирования
е – погрешность вычисления
zn – текущее значение интеграла
zn2 – значение интеграла при числе прямоугольников вдвое меньшем
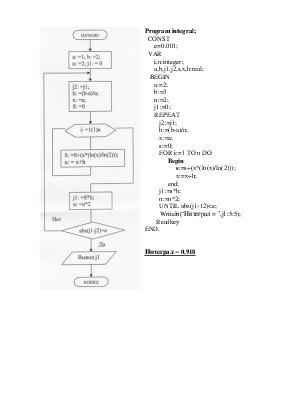
 Program
integral;
Program
integral;
CONST
e=0.001;
VAR
i,n:integer;
a,b,j1,j2,s,x,h:real;
BEGIN
a:=2;
b:=3
n:=2;
j1:=0;
REPEAT
j2:=j1;
h:=(b-a)/n;
x:=a;
s:=0;
FOR i:=1 TO n DO
Begin
s:=s+(x*(ln(x)/ln(2)));
x:=x+h;
end;
j1:=s*h;
n:=n*2;
UNTIL abs(j1-12)<e;
Writeln(‘Интеграл = ’,j1:5:5);
Readkey
END.
Интеграл = 0.918
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.