Теория электрической связи: Методические указания к практическим занятиям

радиотехнической цепи связан со входным сигналом X соотношением Y = 2 – 3X. Числовые характеристики входного сигнала:

m_x = – 1,      D_x = 4.

Определить:

·  математическое ожидание и дисперсию выходного сигнала Y;

·  корреляционную функцию и нормированную корреляционную функцию X и Y.

6.42. Отсчеты мгновенных значений помехи X распределены по гауссовскому закону:

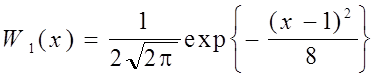
Отсчеты регулярного измерительного сигнала Y, передаваемого по каналу связи, распределены равномерно в интервале (0, 2), X иY независимы.

Определить:

1) M[X+Y];          2) M[XY];         3) M[X²];         4) M[X–Y²];

5) D[X+Y];          6) D[X–Y].

6.43. По тропосферному каналу связи передается N сообщений; длительность каждого сообщения случайна, имеет постоянное математическое ожидание m, дисперсию D и не зависит от длительности других сообщений. Найти математическое ожидание и дисперсию суммарного времени T, за которое будут переданы все N сообщений. Найти T_max – максимальное практически возможное время передачи всех сообщений.

6.44. Производятся четыре независимых измерения суммы сигнала и помехи X на выходе канала связи. Каждое измерение характеризуется одним и тем же математическим ожиданием m_x и средним квадратическим отклонением  s_x .

Результаты измерений: X₁, X₂, X₃, X₄. Рассматриваются разности между соседними измерениями:

Y₁ = X₂ – X₁ ;                   Y₂ = X₃ – X₂ ;                   Y₃ = X₄ – X₃.

Найти характеристики системы этих случайных величин:

·  математическое ожидание m_Y1; m_Y2; m_Y3;

·  среднее квадратическое отклонение s²_Y1; s²_Y2; s²_Y3;

·  нормированную корреляционную матрицу || r_ij ||.

6.45. Дискретные случайные величины X₁, X₂, ..., X₂₄, характеризующие поток вызовов, поступающих на междугородную телефонную станцию в разные часы суток, независимы и распределены по законам Пуассона с параметрами l₁, l₂,.., l₂₄.

Показать, что их сумма

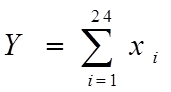
также распределена по закону Пуассона с параметром

.

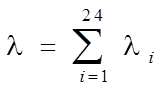6.46. Отсчеты мгновенных значений флуктуационной помехи (X, Y) при двухлучевом распространении радиосигнала в ионосфере распределены по гауссовскому закону с характеристиками m_x, m_y, s_x, s_y и r_xy. Отсчеты мгновенных значений помехи на выходе приемного устройства (U, V) связаны с (X, Y)  зависимостью:

U = ax + by + c,               V = kx + ly + m.

Найти закон распределения системы случайных величин (U, V).

6.47. Для повышения достоверности сигнал одновременно передается по n каналам многоканальной системы связи. Случайный сигнал X имеет равномерное распределение на интервале (1, 2).

Рассматривается среднее арифметическое наблюдаемых значений случайного сигнала X:

.

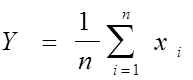На основе закона больших чисел выяснить, к какому числу a будет приближаться (сходиться по вероятности) величина Y при n ® ¥. Оценить максимальную практически возможную ошибку равенства Y » a.

6.48. Случайные величины X и Y, характеризующие поток вызовов на две АТС, независимы и распределены по законам Пуассона с параметрами a и b. Найти закон распределения их разности Z = X – Y и модуля их разности U = |X – Y| = |Z|.

6.49. Отсчеты мгновенных значений помехи после прохождения через две нелинейные радиотехнические цепи распределены по показательному закону с параметрами l и m:

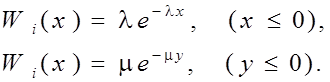
Найти плотность распределения вероятностей разности  Z = X – Y.

6.50. Двумерная плотность распределения вероятностей флуктуационной помехи W₂(X,Y) имеет гауссовский закон распределения:

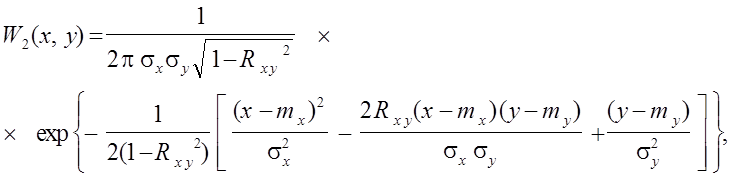
где m_x, m_y, s_x, s_y, R_xy – параметры распределения.

Определить:

·  одномерные плотности распределения вероятностей W₁(x), W₁(y);

·  условные плотности распределения вероятностей W₁(y½x), W₁(x½y).

6.51. Дискретный случайный телеграфный сигнал принимает значения