|
Задание
№1.25
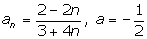
Покажем,
что для любого 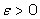 существует такой номер существует такой номер 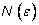 , что , что 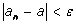 для всех для всех 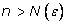 . .

Из
последнего неравенства следует, что можно выбрать 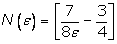 (квадратные
скобки означают целую часть) и при любых (квадратные
скобки означают целую часть) и при любых 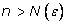 будет
выполняться неравенство будет
выполняться неравенство 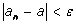 . Значит, по определению предела последовательности . Значит, по определению предела последовательности
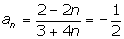 . .
|
|
Задание
№1.26
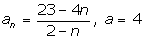
Покажем,
что для любого 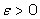 существует такой номер существует такой номер 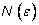 , что , что 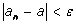 для всех для всех 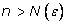 . .

Из
последнего неравенства следует, что можно выбрать 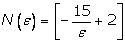 (квадратные
скобки означают целую часть) и при любых (квадратные
скобки означают целую часть) и при любых 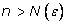 будет
выполняться неравенство будет
выполняться неравенство 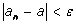 . Значит, по определению предела последовательности . Значит, по определению предела последовательности
 . .
|
|
Задание
№1.27
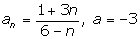
Покажем,
что для любого 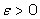 существует такой номер существует такой номер 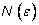 , что , что 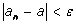 для всех для всех 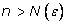 . .

Из
последнего неравенства следует, что можно выбрать 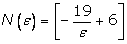 (квадратные
скобки означают целую часть) и при любых (квадратные
скобки означают целую часть) и при любых 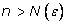 будет
выполняться неравенство будет
выполняться неравенство 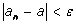 . Значит, по определению предела последовательности . Значит, по определению предела последовательности
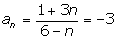 . .
|
|
Задание
№1.28
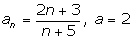
Покажем,
что для любого 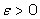 существует такой номер существует такой номер 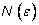 , что , что 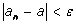 для всех для всех 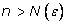 . .
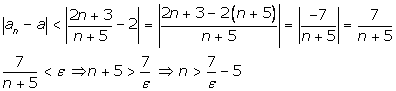
Из
последнего неравенства следует, что можно выбрать 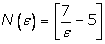 (квадратные
скобки означают целую часть) и при любых (квадратные
скобки означают целую часть) и при любых 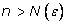 будет
выполняться неравенство будет
выполняться неравенство 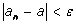 . Значит, по определению предела последовательности . Значит, по определению предела последовательности
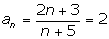 . .
|
|
Задание
№1.29
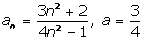
Покажем,
что для любого 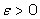 существует такой номер существует такой номер 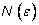 , что , что 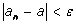 для всех для всех 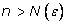 . .

Из
последнего неравенства следует, что можно выбрать 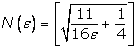 (квадратные
скобки означают целую часть) и при любых (квадратные
скобки означают целую часть) и при любых 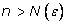 будет
выполняться неравенство будет
выполняться неравенство 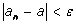 . Значит, по определению предела последовательности . Значит, по определению предела последовательности
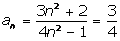 . .
|
|
Задание
№1.30
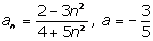
Покажем,
что для любого 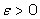 существует такой номер существует такой номер 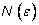 , что , что 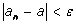 для всех для всех 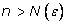 . .

Из
последнего неравенства следует, что можно выбрать 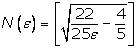 (квадратные
скобки означают целую часть) и при любых (квадратные
скобки означают целую часть) и при любых 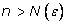 будет
выполняться неравенство будет
выполняться неравенство 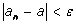 . Значит, по определению предела последовательности . Значит, по определению предела последовательности
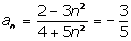 . .
|
|
Задание
№1.31
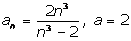
Покажем,
что для любого 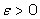 существует такой номер существует такой номер 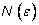 , что , что 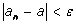 для всех для всех 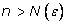 . .

Из
последнего неравенства следует, что можно выбрать 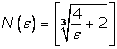 (квадратные
скобки означают целую часть) и при любых (квадратные
скобки означают целую часть) и при любых 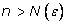 будет
выполняться неравенство будет
выполняться неравенство 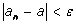 . Значит, по определению предела последовательности . Значит, по определению предела последовательности
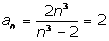 . .
|