Структурный и кинематический анализ зубчатого привода, страница 5

мм

мм

    Радиус закругления зуба:

 мм.

   Строим зубчатое зацепление в масштабе:

 м/мм.

Определяем коэффициент перекрытия колеса.

>1,1

Условие выполняется

    3. 2 Определение передаточного отношения:

    общее                                           ,

    зубчатого ряда                             ,                           

    планетарного редуктора             .

   3. 3 Определение чисел зубьев колес планетарного зацепления

   Из уравнения передаточного отношения:

              ,

находим значение дроби .

         Откуда:    ,       

                           ,

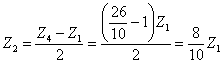Принимаем Z₁=30, тогда  Z₂ = 24, Z₄ =78.

      Выберем максимально возможное число сателлитов из условия соседства:                      

                          

      Неравенство выполняется при  

      Условие сборки    

      Условие сборки  выполняется при К=3 и р = 0.

       Все условия выполняются, значит принимаем выбранные числа зубьев.

       Вычерчиваем две проекции схемы механизма в масштабе  м/мм.

       Скорость точки А:

м/с;

м/смм.

Нахдим r плана линейных скоростей

Где: m=2 для r_1.2.3

 

 

Отрезки на прямой х-х Р1, Р(2-3), Р(Н-5), Р6 изображают в масштабе  угловые скорости соответствующих звеньев. Находим угловую скорость и число оборотов.

Находим относительную ошибку

%

%

%

Ошибка вычислений не должна превышать 5%