Вычисление корреляционной таблицы эмпирического распределения двумерной СВ, страница 6

Y²_наиб = 2,26

Y²_кр (a,n) = 12,592

Y²_наиб <Y²_кр

8. Найдем интервальные оценки параметров нормального закона распределения

1 - a = g = 0,95

n = n – 1 = 100 – 1 = 99

t_g = 1,984

Погрешность интервального оценивания:

e_y = t_g* S_y/n^1/2 = 0,99

y – e_y <M(y)< y + e_y

24,34 – 0,99<M(y)<24,34 + 0,99

23,35<M(y)<25,33

Среднее квадратическое отклонение s

1 - a = g = 0,95

n = n – 1 = 100 – 1 = 99

g₁ = 0,88

g₂ = 1,16

g₁ * S_y < s <g₂ * S_y

0,88*5 < s < 1,16*5

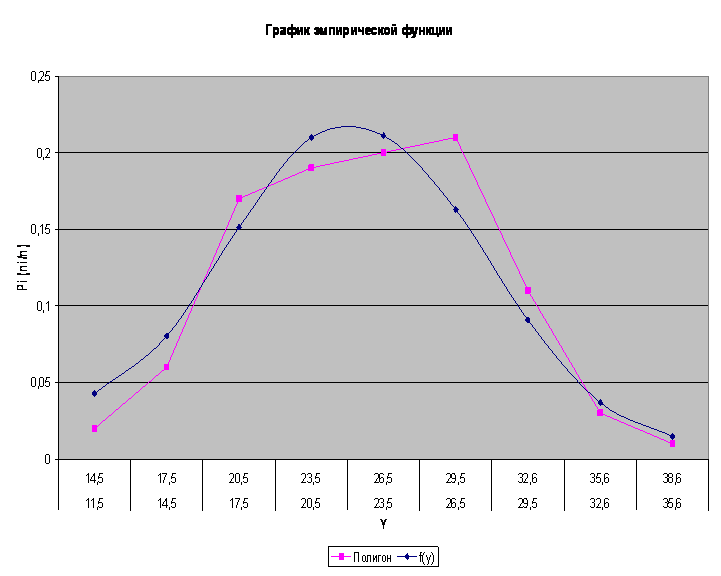
9. Кореляционный анализ выборочных данных СВ X и Y.

а) Составим корреляционную таблицу.

Таблица для частот n_xy пар значений (x_i;y_i)

	X	10,1	19,9	29,7	39,5	49,3	59,2	69,0	78,8	88,6
Y		19,9	29,7	39,5	49,3	59,2	69,0	78,8	88,6	98,40
11,5	14,5	1	1	0	0	0	0	0	0	0
14,5	17,5	2	3	1	0	0	0	0	0	0
17,5	20,5	1	4	5	5	2	0	0	0	0
20,5	23,5	0	1	9	8	1	0	0	0	0
23,5	26,5	0	0	1	7	6	6	0	0	0
26,5	29,5	0	0	0	1	7	8	5	0	0
29,5	32,6	0	0	0	0	1	3	4	3	0
32,6	35,6	0	0	0	0	0	1	1	1	0
35,6	38,6	0	0	0	0	0	0	0	0	1