Типовой пример расчета напряженно-деформированного состояния изгиба стержня с учетом свойств ползучести

1.  ТИПОВОЙ ПРИМЕР РАСЧЕТА НДС ИЗГИБА СТЕРЖНЯ С УЧЕТОМ СВОЙСТВ ПОЛЗУЧЕСТИ

Рассмотрим задачу  о ползучести стержня прямоугольного поперечного сечения, изгибаемого парами сил.

Установившаяся ползучесть. Направим ось zпо оси стержня (рис. 1);

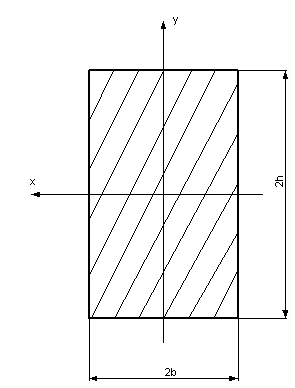пусть изгибающий момент действует в плоскости yz. По соображениям симметрии плоские сечения, нормальные к оси z до деформации, будут плоскими и нормальными к оси стержня и после деформации; поэтому

                                ,                                  (1)

где через kобозначена установившаяся скорость изменения кривизны оси.

Напряжения   должны удовлетворять уравнению равновесия

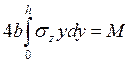                          ,                               (2)

где М>0 – изгибающий момент.

По закону ползучести во втором (установившемся) периоде имеем

                                                                                                 (3)

или

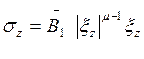                                                   ,                                            (4)

где обозначено

.                     

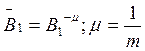Внося  и , согласно выражениям (4) и (1), в уравнение равновесия, получаем

                                                     ,                                               (5)

где  - обобщенный момент инерции:

.

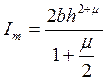При m= 1 обобщенный момент инерции переходит в обычный момент инерции I_1, фигурирующий в сопротивлении материалов. Согласно (4) находим

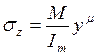                                                       .                                                (6)

В области отрицательных yнапряжение продолжается нечетным образом.

В случае линейной упругости напряжения при изгибе зависят линейно от координаты y.

Представим решение данной задачи в MSC.Patran, Marc.

Стержень имеет размер 1х1х10мм, модуль упругости ,

коэффициент Пуассона , степенной закон ползучести , , .

Построим геометрию 3D стержня в следующем виде:

Geometry / Create / Surface / XYZ / Vector Coordinates List: <0.5 0.5 0>, Origin Coordinates List: [0 0 0] / Apply

Geometry / Create / Surface / XYZ / Vector Coordinates List: <-0.5 0.5 0>, Origin Coordinates List: [0 0 0] / Apply

Geometry / Create / Surface / XYZ / Vector Coordinates List: <-0.5 -0.5 0>, Origin Coordinates List: [0 0 0] / Apply

Geometry / Create / Surface / XYZ / Vector Coordinates List: <0.5 -0.5 0>, Origin Coordinates List: [0 0 0] / Apply .

Geometry / Create / Solid / Extrude / Solid Type: IsoMeshable, Translation Vector <0 0 10>, Surface List: Surface 1:4 / Apply (рис.1).

Для последующей разбивки изопараметрическими элементами Hex, нужно преобразовать полученную трехмерную геометрию в трипарметрическую.

Geometry / Edit / Solid / Refit / Option: To TriParametric / Solid List: Solid 1:4 / Apply.

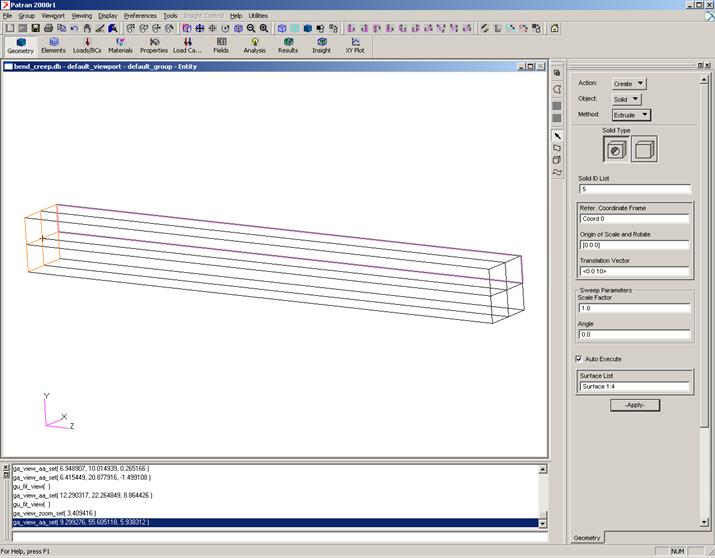
Рис.1

Зададим граничные условия для геометрической модели. Зафиксируем конец стержня по перемещениям y,z, и от изгибов в плоскости yz (т.е. продольное сечение стержня закрепляем по x):

Loads/BCs / Create / Displacement / Nodal / New Set Name : x / Input Data / Translations <T1 T2 T3>: <0,,     > / OK / Select Application Region / выбираемпродольноесечение / OK / Apply (рис.3-4).

Loads/BCs / Create / Displacement / Nodal / New Set Name : yz / Input Data / Translations <T1 T2 T3>: <,0,0 >  / OK / Select Application Region… / OK / Apply (рис.2).

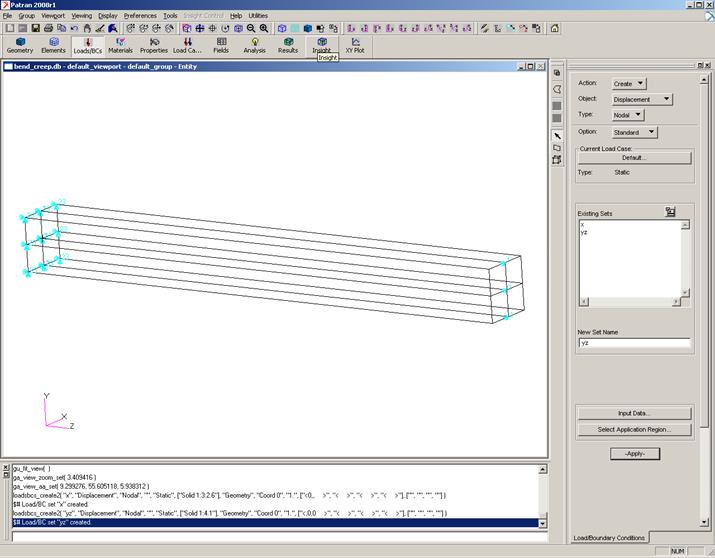
Рис.2

Для задания момента в виде напряжений , необходимо задать поле (функцию) по координате y:

Fields / Create / Spatial / PCL Function / Field Name : Sz / Scalar Function: -'Y*700 / Apply

Нагрузка давлением определяется в виде:

Loads/BCs / Create / Pressure / Nodal / New Set Name : press / Input Data … / OK / Select Application Region… / OK / Apply (рис.3).

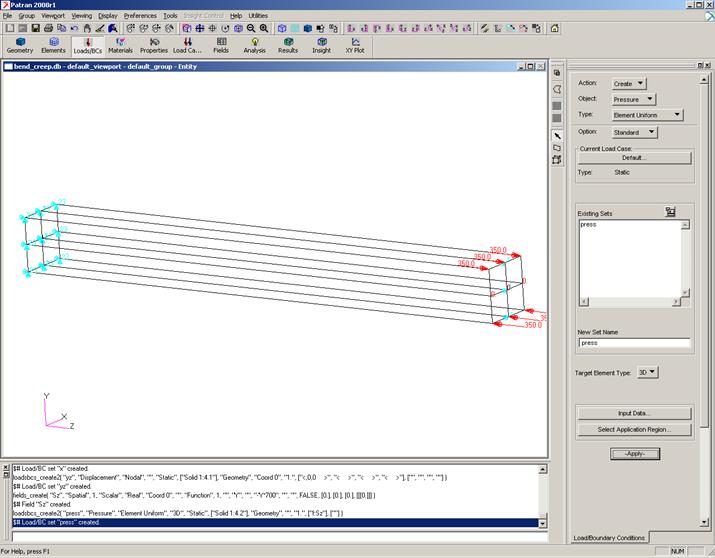
Рис.3

Создаем сетку элементами Hex8, определяя количество элементов на гранях:

Elements / Create / Mesh Seed / Uniform / Number of Elements: 3 / Curve List / Укажите поочередно ребра поперечного сечения/ Apply .

Elements / Create / Mesh / Solid / Elem Shape: Hex; Mesher: IsoMesh; Topology: Hex8; Solid List/ Укажите необходимую геометрию / Apply.

После создания сетки конечных элементов нужно удалить повторяющиеся узлы: Elements / Equivalence / All / ToleranceCube / Apply(рис. 4).

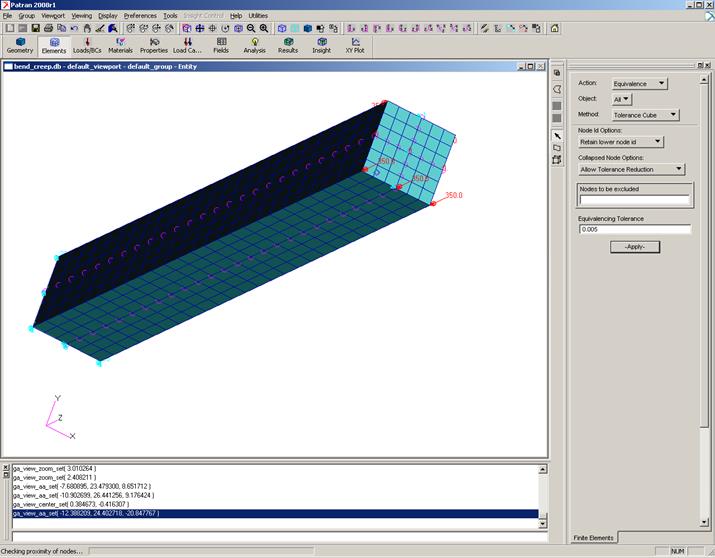
Рис.4

Создание изотропного упругого материала: Materials / Create / Isotropic / Manual Input / Material Name : m / Input Property… / Constitutive Model : Linear Elastic / Elastic Modulus = : 7000 /Poisson Ratio = : 0.3 /  OK / Apply.

Определение параметров ползучести материала: Materials / Create / Isotropic / Manual Input / Material Name : m / Input Property… / Constitutive Model : Creep / Coefficient = : 5e-22 /Exponent of Stress  = : 8 /  OK / Apply.

Определение свойств элементов (указания материала для них, опций для решения) возможно путем указания геометрии или элементов: Properties / Create / 3 D / Solid / Property Set Name : pr / нажмите кнопку Input Property / Material Name: m:m / OK / Выберите геометрию или КЭ в поле Select Members : (список тел) / Add / Apply .

Перед началом расчета необходимо указать параметры  решения и вывод результатов.