Типовой пример расчета напряженно-деформированного состояния изгиба стержня с учетом свойств ползучести, страница 2

Analysis / Analyse / Entire Model / Full Run / Load Step Creation… / Solution Type: Creep / Solution Parameters / Nonlinear Geometric Effects: None / Load Increment Params…/

Increment Type: Adaptive Creep, Total Time:3.5, Max. # of Increments Allowed: 10000 /OK /OK (рис.5)

Output Request…/ Select Nodal Results…/ выбрать Displacement (1) / OK (рис.6)

Select Element Results…/ Strain, Total Components (301); Stress, Components (311); Strain, Crepp Components (331); Strain, Elastic Components (401) /OK  /OK /Apply  (рис.7)

Analysis / Analyse / Entire Model / Full Run / Job Parameters… / (рис.8)  / OK / Apply.

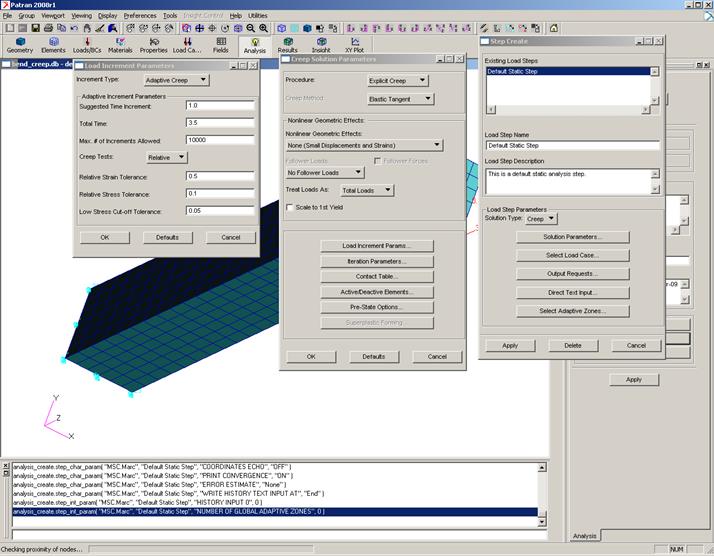
Рис.5

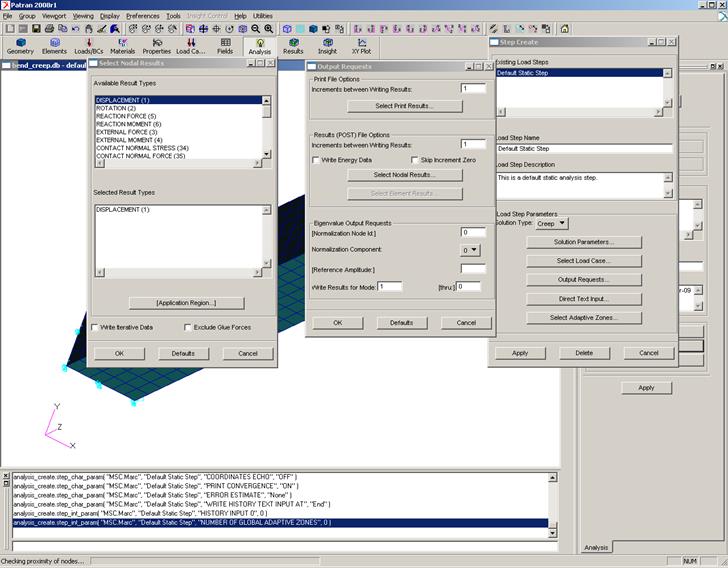
Рис.6

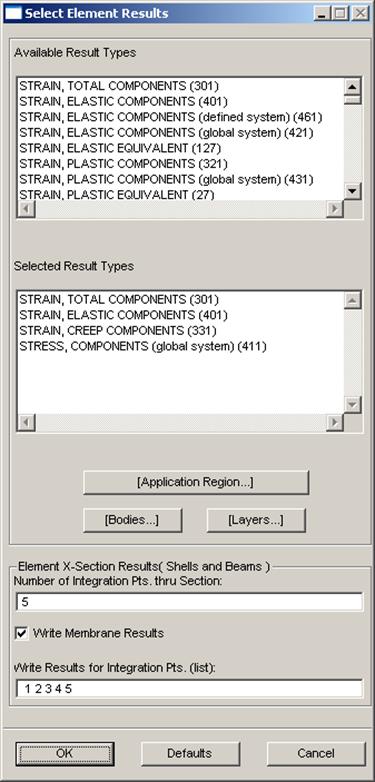
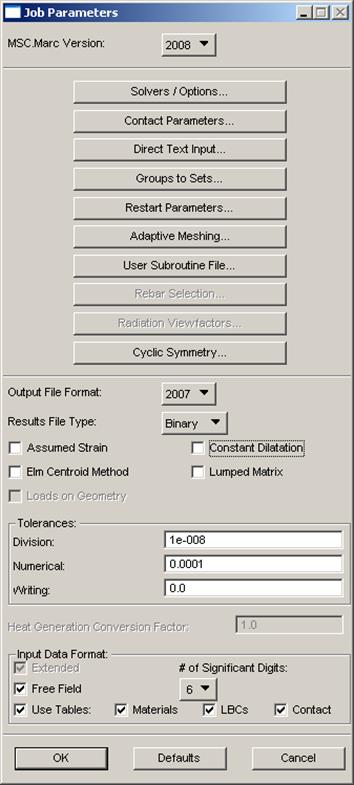
                          Рис.7                                                      Рис.8

После расчета загружаем файл расчета

Analysis / Read Results / Results Entities / Attach / Select Results File / выбрать файл результатов / OK / Apply.

Деформации ползучести и напряжения в направлении оси стержня  представлены на рис.9-10.

Для построения графика распределения напряжения в поперечном сечении необходимо выполнить следующую команду:

Results / Create / Graph / Y vs X / Select Result Cases: выбратьконечныйрезультат / Select Y Result: Stress ; Quantity: Z Component / X: Coordinate : Coord 0.2/

Нажав иконку Target Entities выбрать в меню узлы или элементы конца стержня / Apply (рис.11).

В случае линейно упругости, в отличие от ползучести, распределение напряжений должно быть линейным.

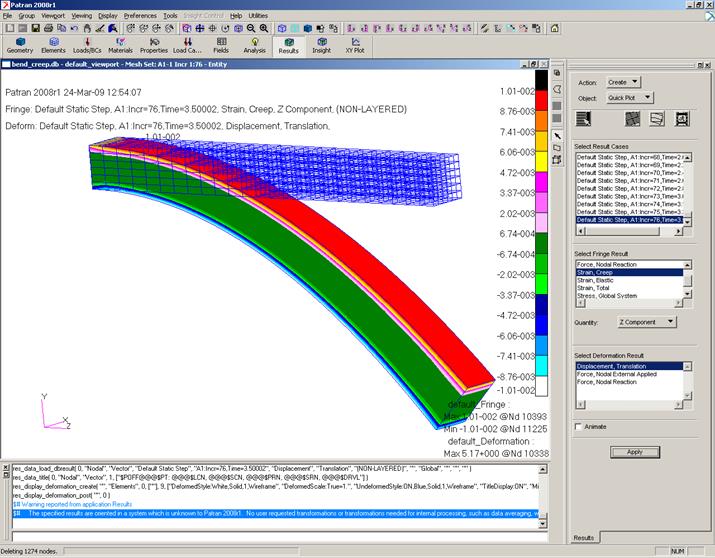
Рис.9

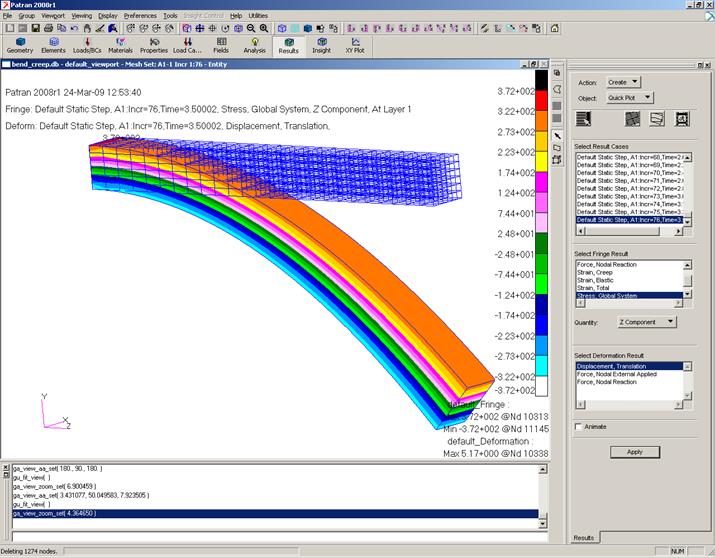
Рис.10

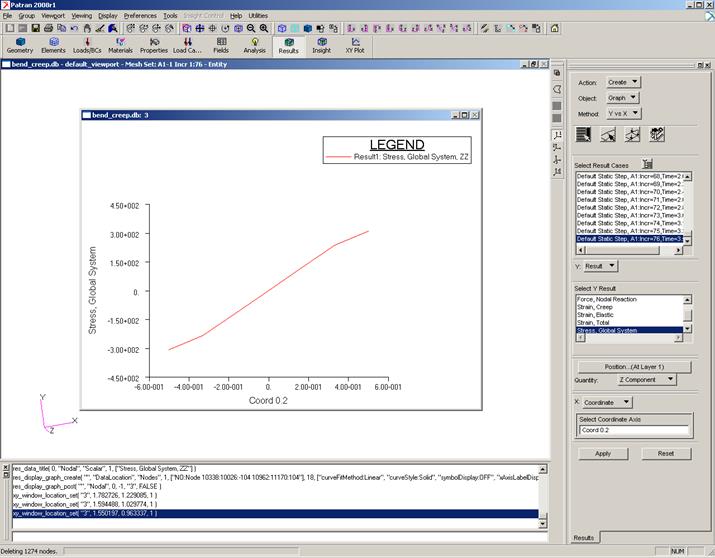
Рис.11

          Релаксация изгибающего момента. Пусть при  t=0 стержень был изогнут моментом М₀ , после чего концы балки были жестко закреплены. Изгибающий момент М постепенно релаксирует.

Полное уравнение ползучести, с учетом упругих деформаций имеет вид

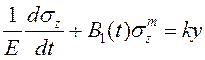                                                                    ,                                                           (7)

где E – модуль упругости.                                 

          Вследствие независимости от координаты z конфигурация стержня при t>0 не изменяется, поэтому k=0 и из уравнения (7) вытекает дифференциальное уравнение

,

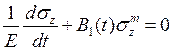Следовательно, после интегрирования

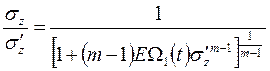                                        ,                                  (8)

где  - начальное напряжение в том же волокне балки,

Если , т.е. не зависит от времени, то

.

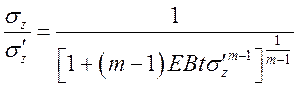Для проведения релаксации можно воспользоваться опцией переноса результатов предыдущего расчета. Для этого модифицируем первоначальную модель изгиба стержня: вместо давления фиксируются перемещения по z (рис.12).

Перед началом расчета необходимо указать параметры решения и файл предыдущего расчета..

Analysis / Analyse / Entire Model / Full Run / Load Step Creation… / Solution Type: Creep / Solution Parameters / Nonlinear Geometric Effects: None / Load Increment Params…/

Increment Type: Adaptive Creep, Total Time:3.5, Max. # of Increments Allowed: 10000 /OK /

Pre-State Options…/ 2D to 2D/3D to 3D / Move Results : Stress, Displ.,Vel.,Accel. / Post File Options: Last Increment / Select File / выбрать нужный файл.

/ OK / Apply. (рис.13).

После расчета присоединяем файл результатов и создаем график изменения напряжений с течением времени для конкретного узла (рис.14).

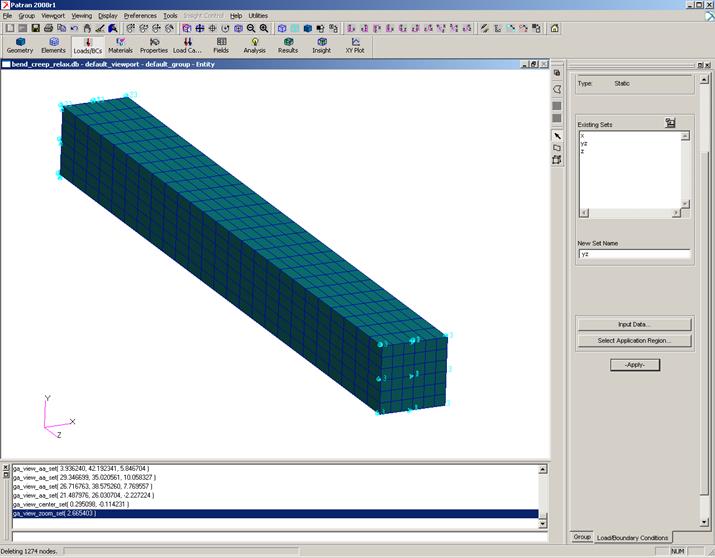
Рис.12

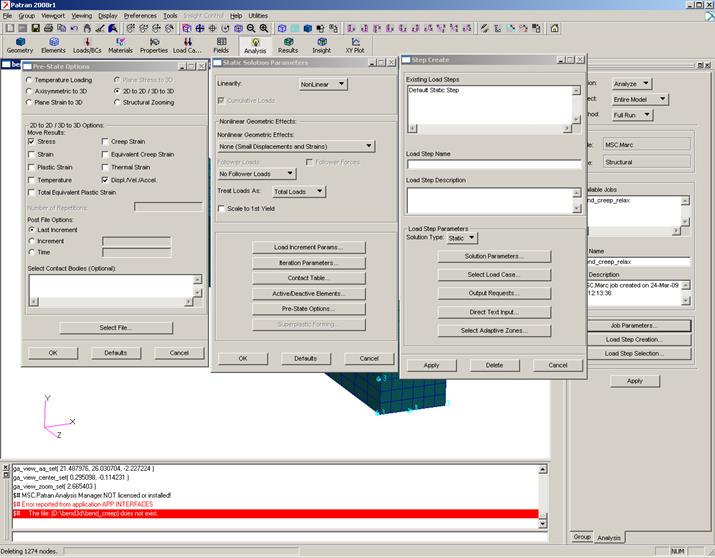
Рис.13

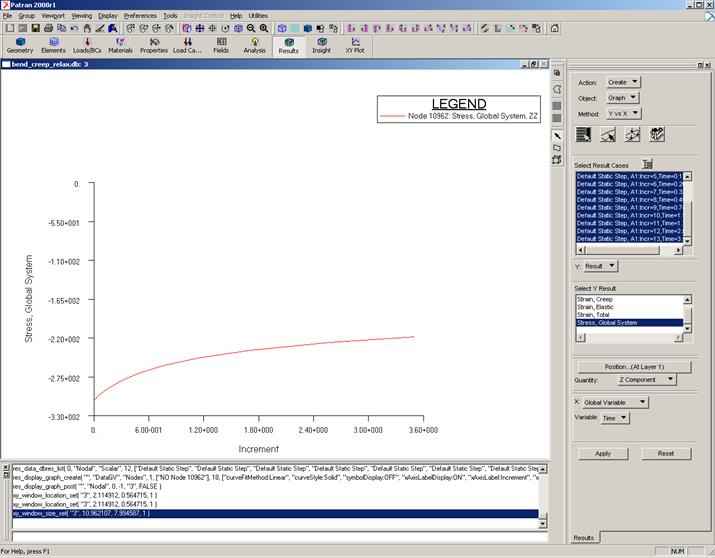
Рис.14

2.  ВАРИАНТЫ РАСЧЕТНО-ГРАФИЧЕСКИХ ЗАДАНИЙ «ИЗГИБ СТЕРЖНЯ С УЧЕТОМ СВОЙСТВ ПОЛЗУЧЕСТИ».

Стержень имеет профиль представленный в табл. 1, табл.2, длиной 10м, модуль упругости , коэффициент Пуассона , степенной закон ползучести , , .

Табл.1

№	схема	№	схема
1		2
3		4
5		6
7		8
9		10

Табл.2

Номер схемы	a, м	b, м	c, м	d, м
1	1	-	-	-
2	1	2	-	-
3	0.5	2	1	0.5
4	0.5	2	2	0.5
5	0.4	2.2	0.6	0.8
6	1	1.5	3	-
7	2	0.5	2	0.5
8	2.5	1.5	-	-
9	2.2	1.8	-	-
10	1	1.4	2.5	-

Отчет должен содержать краткое описание:

1)  аналитическое решения распределения напряжений при установившейся ползучести и релаксации

2)  построения геометрической модели в MSC.Patran;

3)  функций генерации конечно-элементной сетки;

4)  задания граничных условий;

5)  свойства материала;

6)  методы расчета, критерии сходимости;

7)  сообщений MSC.Marc о завершении расчета или ошибках;

8)  особенностей распределения всех компонент напряжений, упругих и пластических деформаций, перемещений.

9)  график распределения напряжений по сечению стержня при установившейся ползучести и график изменения напряжения в характерной точке сечения с течением времени релаксации.