Анализ напряжений, деформаций и перемещений в упругих телах в MSC.PATRAN и MSC.NASTRAN

УДК 539.3

Л.В.Нагаева, студентка; А.И. Олейников, докт.физ.-мат. Наук, профессор

Комсомольский – на – Амуре государственный технический университет

АНАЛИЗ НАПРЯЖЕНИЙ, ДЕФОРМАЦИЙ И ПЕРЕМЕЩЕНИЙ В УПРУГИХ ТЕЛАХ В MSC. PATRAN И MSC. NASTRAN НА ПРИМЕРЕ ИЗГИБА СТЕРЖНЯ.

Задачей изгиба стержня интересовался еще Леонардо да Винчи. Он установил, что в двухопорной балке постоянного поперечного сечения «изгибается больше всего» та часть, которая находится на наибольшем расстоянии от опор.

Задача прочности изогнутого прямого стержня прямоугольного поперечного сечения была поставлена Г. Галилеем.

Правильное решение задачи об изгибе балки было дано А. Параном в 1713г. Исследование Парана повторил в 1729г Г. Бюльфингер в работе, опубликованной в 1735г, а затем и Ш. Кулон в 1773г. Они, по видимому ,не знали о работах Парана.

Так же задачей изгиба занимались А. Дюло (1820 г), Томас Тредгольд (1821 г), Л. Навье (1826 г, замечу, что Л. Навье не определил понятие момента инерции площади поперечного сечения. Оно было введено инженером Н. Перси в 1834 г., который разработал теорию моментов инерции), И. Ходкинсон (1824), Сен – Венан  (1863г) и другие.

Но и сейчас эта задача остается актуальной. Сейчас нам на помощь при решении задач приходят интерактивные программы графического представления информации, позволяющих более наглядно и легко описывать геометрические и физические свойства объектов, программные комплексы, основанные на чис­ленных методах, например, MSC.Nastran, MSC.Marc, MSC.Patran и др.

Рассмотрим два стержня – квадратного и круглого поперечного сечения. Предположим, что температура стержня одинакова во всех точках, атмосферным давлением можем пренебречь и объемные силы отсутствуют.  Существует только одно внешние воздействие, а именно изгибающий момент М, которые будут действовать, в одной из главных плоскостей двумя равными и противоположными моментами М. Определим начало координат в центре тяжести поперечного сечения, а плоскость xz — в главной плоскости изгиба.

В теории упругости уже известно аналитическое решение для балки. Закрепим балку жестко на левом торце (исключим перемещения вдоль осей Z и X), и исключим изгиб в плоскости YZ, к правому торцу приложим изгибающий момент.

Рассмотрим искомое решение для напряжений в виде:

,    

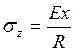Где R – радиус кривизны стержня после изгиба.

Представлю решение данной задачи в MSC.Patran, Nastran.Модуль упругости Е = 7000 кГ/мм²,  коэффициент Пуассона v = 0.3, радиус кривизны стержня после изгиба R = 10 мм.

Чтоб было возможным произвести сравнительный анализ, создаю балки с максимально одинаковыми параметрами. Длина балки 10 мм, размер прямоугольного сечения – 1х1 мм, радиус круглого поперечного сечения – 0,5 мм. Обе балки были разбиты на конечную сетку методом Hex8, число конечных элементов для обеих балок – 200.

Для задания момента в виде напряжений 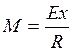 задаемся полем (функцией) по координате Х, приняв числовое значение равное 700.

Рассмотрим задачу в линейной геометрической постановке – при малых перемещениях, прогибах и поворотах элементов.

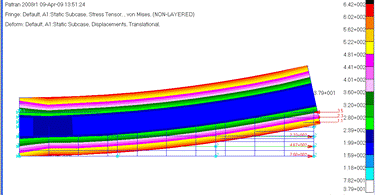
Полученные результаты совпадают с аналитическим решением (я убедилась, что прогиб в балке с круглым поперечным сечением меньше, чем в балке с прямоугольным). На графике распределения напряжений VON MISES отлично виден нейтральный слой, возникновение концентрации напряжений во внешних волокнах и вблизи заделки.

В дальнейшем планируется рассмотреть данную задачу уже в нелинейной постановке – при больших перемещениях, прогибах и поворотах элементов.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

К.С. Бормотин, Анализ напряженно – деформированного состояния в системе MSC. Patran & MSC. Nastran: учеб. пособие/ К.С.Бормотин, А.И. Олейников. – Комсомолькн – на – Амуре: ГОУВПО «КнАГТУ» - 2009. – 135с.