Механика \ Строительная механика

Строительная механика: Методические указания к самостоятельной работе, страница 4

Номер строки

d,

м

h,

м

Номер панели, считая слева

Грузовой

пояс

Нагрузка q, кН/м

постоянная

временная

1

2

3

4

5

6

7

8

9

0

3,5

4,0

4,5

5,0

4,0

5,0

3.5

4,0

4.5

5,0

3,0

3,0

3,0

3,5

3,5

3,5

4,0

4,0

4,0

3,5

3

3

4

4

3

3

4

3

4

3

верхний

нижний

верхний

нижний

верхний

нижний

верхний

нижний

верхний

нижний

10

15

20

10

15

20

10

15

20

15

20

10

15

20

15

20

10

20

15

20

б

в

в

б

в

а

Задача 5. Определение перемещений в многопролётной

статически определимой балке.

Для балки (см. рисунок 2), рассмотренной в задаче 1, требуется:

а) определить вертикальные перемещения незакреплённых (из семи обозначенных) сечений, полагая жёсткость всех частей EI = const;

б) изобразить изогнутую ось балки, используя найденные значения вертикальных перемещений и согласуя её с эпюрой изгибающих моментов.

Задача 6. Определение перемещений в статически

определимой раме.

Для рамы (см. рисунок 3), рассмотренной в задаче 2, требуется:

а) определить одно из возможных линейных перемещений незакреплённого узла (узел выбрать самостоятельно);

б) определить угол поворота всего узла (если узел жёсткий), или угол поворота жёсткой части комбинированного узла. Принять жёсткости
EIриг = 2EIст.

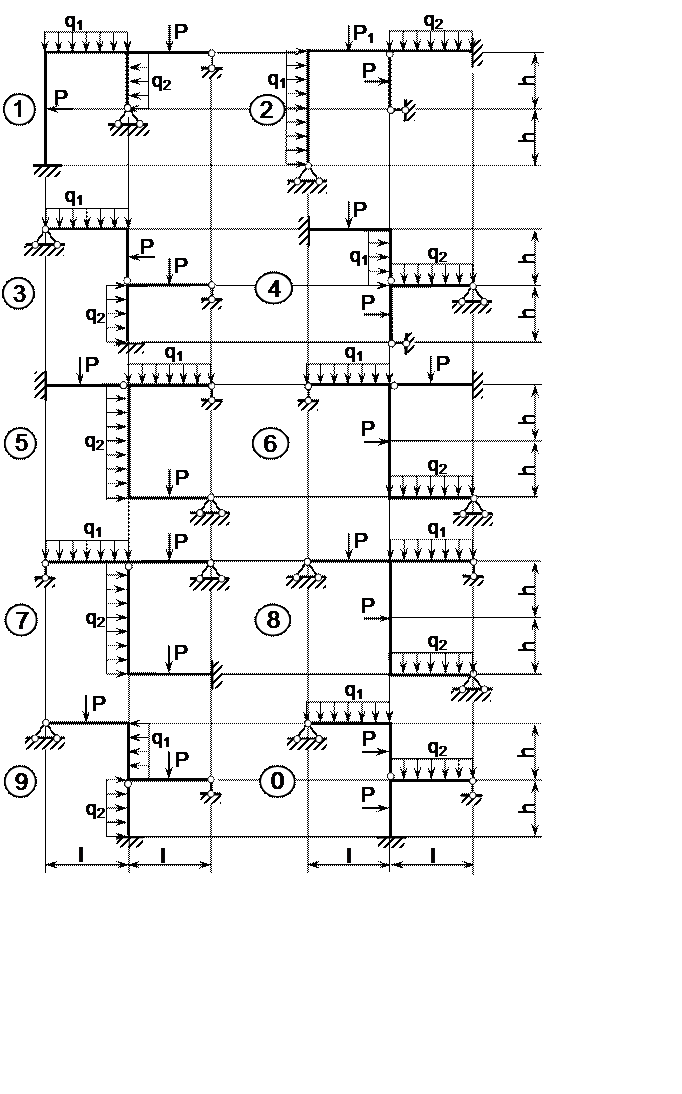
Задача 7. Расчёт плоской статически неопределимой рамы

методом сил.

Для рамы (рисунок 6), размеры, соотношение изгибных жёсткостей ригелей и стоек и нагрузка которой выбирается из таблицы 6, требуется:

а) построить эпюры изгибающих моментов, поперечных и продольных сил, раскрыв статическую неопределимость;

б) проверить правильность раскрытия статической неопределимости.

Задача 8. Определение перемещений в статически

неопределимой раме.

Определить возможные линейные и угловые перемещения жёстких и комбинированных узлов рамы, рассмотренной в задаче 7.

Таблица 6 - Исходные данные к задачам 7, 8, 9

Номер строки

l,

м

h,

м

P1,

кН

P2,

кН

q1,

кН/м

q2,

кН/м

EIст:EIриг

1

2

3

4

5

6

7

8

9

0

4

5

6

4

5

6

4

5

6

4

3

4

5

6

3

4

5

6

3

4

20

30

40

50

60

20

30

40

50

60

20

-40

60

-80

100

-80

40

-60

80

100

-16

24

-32

40

-40

16

-24

32

-40

40

32

32

32

32

32

40

40

40

40

40

1,0:1,5

1,0:2,0

1,0:2,5

1,5:1,0

2,0:1,0

2,5:1,0

1,0:1,5

1,0:2,0

1,0:2,5

2,0:1,0

б

в

а

б

в

б

в

Примечание. Силы P1 и P2 приложены посередине соответствующих участков рамы.


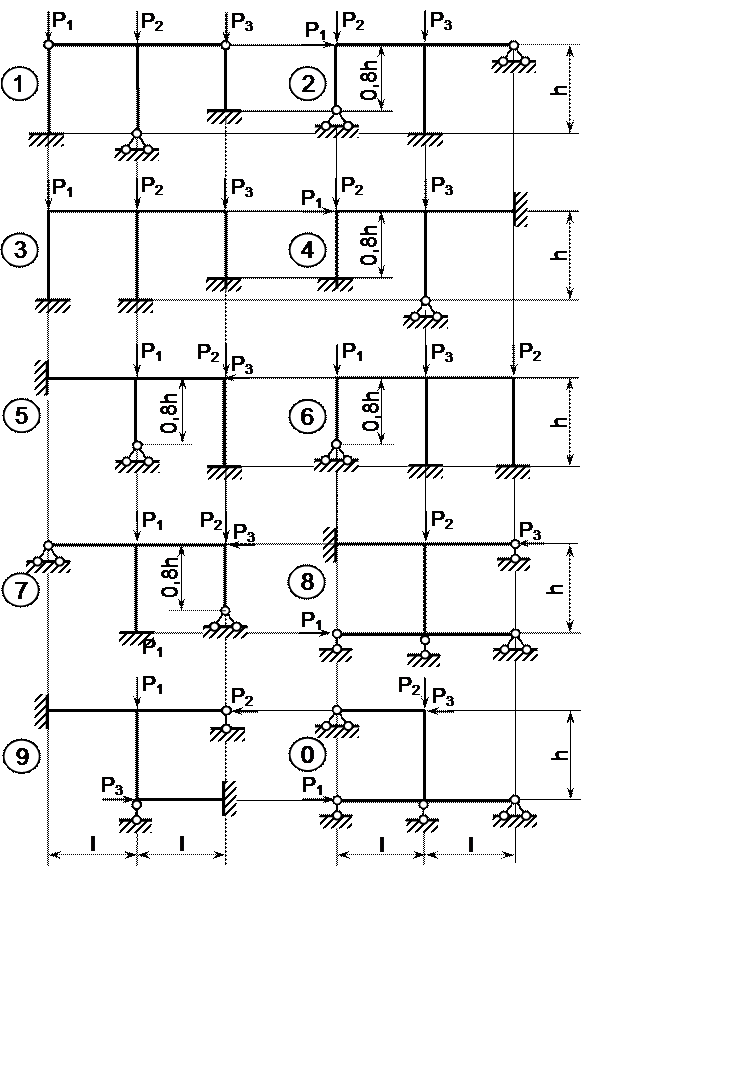
Рисунок 6 - Расчётные схемы к задачам 7, 8 и 9
 

Задача 9. Расчёт плоской статически неопределимой рамы

методом перемещений.

Для той же рамы, что и в задаче 7 (см. рисунок 6), требуется:

а) построить эпюру изгибающих моментов, раскрыв кинематическую неопределимость;

б) проверить правильность раскрытия кинематической (и, соответственно, статической) неопределимости.

Задача 10. Расчёт устойчивости плоской рамы методом

перемещений.

Для рамы (рисунок 7), размеры, соотношение изгибных жёсткостей ригелей и стоек и нагрузка которой выбираются из таблицы 7, требуется:

а) определить критическое значение параметра нагрузки Pкр = P1;

б) изобразить форму потери устойчивости.

Таблица 7 - Исходные данные к задаче 10

Номер строки

l,

м

h,

м

P2/P1

P3/P1

EIст/EIриг

1

2

3

4

5

6

7

8

9

0

3.0

4,5

6,0

3,0

4.5

6,0

3,0

4,5

6,0

3,0

4,5

6,0

3,0

4,5

6,0

3,0

4,5

6,0

3,0

4,5

0

0

0

0

0

2,2

2,0

1,8

1,6

1,4

1,4

1,6

1,8

2,0

2,2

0

0

0

0

0

0,5

0,6

0,7

0,8

0,9

1,1

1,2

1,3

1,4

1,5

б

в

б

б

в

Скачать файл