|
Номер сечения |
М = М 0- Н·у, кН·м |
Q = Q0 cos φ -H sin φ, кН |
N = -Q0 sin φ -Н cos φ, кН |
||||||
|
М 0 |
-H·y |
M |
Q0 cos φ |
-H sin φ |
Q |
-Q0 sin φ |
-Н cos φ |
N |
|
|
А 1 2л 2п 3 4л 4п 5 6 7 8л 8п 9 10 11 B |
0 570 1140 1140 1510 1840 1840 1860 1840 1780 1680 1680 1300 880 440 0 |
0 -760,6 -1206,8 -1206,8 -1502,6 -1694,9 -1694,9 -1804,4 -1840,0 -1804,4 -1694,9 -1694,9 -1502,6 -1206,8 -760,6 0 |
0 -190,6 -66,8 -66,8 7,4 145,1 145,1 55,6 0 -24,4 -14,9 -14,9 -202,6 -326,8 -320,6 0 |
109,6 182,1 224,6 153,7 155,3 147,5 19,0 0 -20,0 -39,5 -57,1 -171,3 -177,4 -173,4 -140,6 -84,6 |
-212,3 -176,9 -141,5 -141,5 -106,1 -70,8 -70,8 -35,4 0 35,4 70,8 70,8 106,1 141,5 176,9 212,3 |
-102,3 5,2 83,1 12,2 49,2 76,7 -51,8 -35,4 -20,0 -4,1 13,7 -100,5 -71,3 -31,9 36,3 127,7 |
-263,1 -219,2 -175,4 -120,0 -80,8 -47,7 -6,2 0 0 -6,2 -18,5 -55,4 -92,3 -135,4 -169,2 -203,1 |
-88,5 -147,0 -181,3 -181,3 -204,1 -218,8 -218,8 -227,3 -230,0 -227,3 -218,8 -218,8 -204,1 -181,3 -147,0 -88,5 |
-351,6 -366,2 -356,7
-284,9 -266,5 -225,0 -227,3 -230,0 -233,5 -237,3 -274,2 -296,4 -316,7 -316,2 -291,6 |
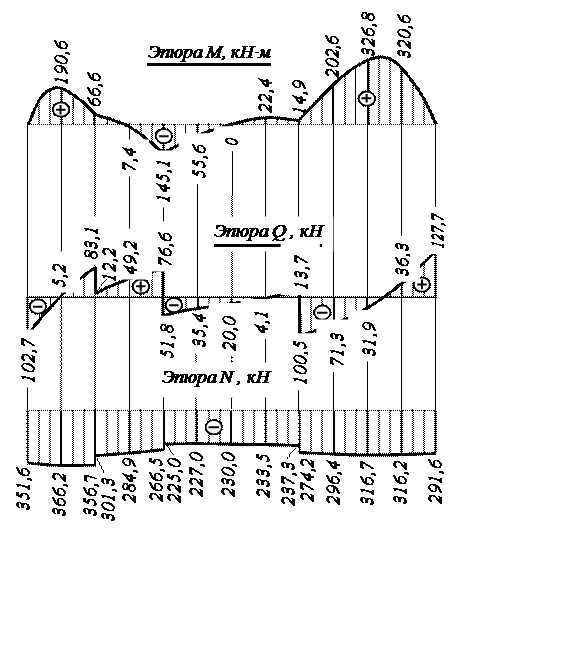
Рис. 8
2.5. Строим линии влияния внутренних усилий в сечении 2
Линий влияния 
(рис.9)
построим, используя линии влияния опорных реакций 
и 
.
а) 
на участке А–2; 
Условно продлив ветви линий влияния за пределы участка А–2 – до опоры В, из выражений (4) получим значения линий влияния под опорой В.
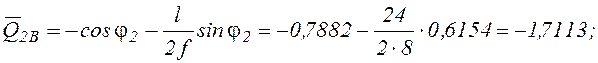
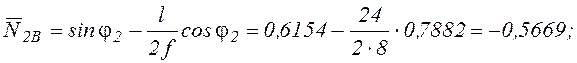
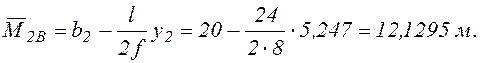
Из
выражений (4) при расположении силы 
на расстоянии
х2=4 м (чуть левее сечения 2) находим
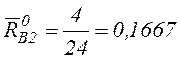; 0 
Значения
можно получить и из геометрических соотношений.
Ветви линий влияния, построенные по этим значениям, обозначим римской цифрой I.
б) на участке 2–С; 
Из выражений (5) получим значения линий влияния под опорами А и В, условно продлив ветви линий влияния до опор.
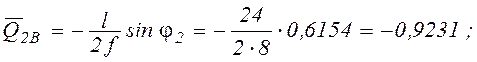
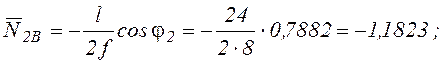
Из геометрических соотношений находим
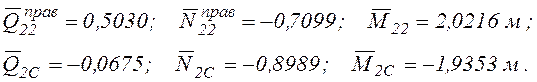
Ветви линий влияния этого участка обозначим римской цифрой II.
в) 
на участке С–В; 
Значения линий влияния над опорами А и В получим из выражений (6), условно продлив ветви за пределы участка С–В – до опоры А.
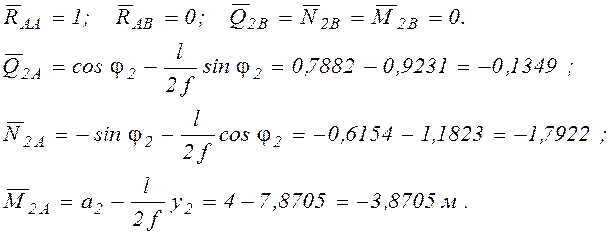
Значения 
получим из
геометрических соотношений.
Ветви линий влияния этого участка обозначим римской цифрой III.
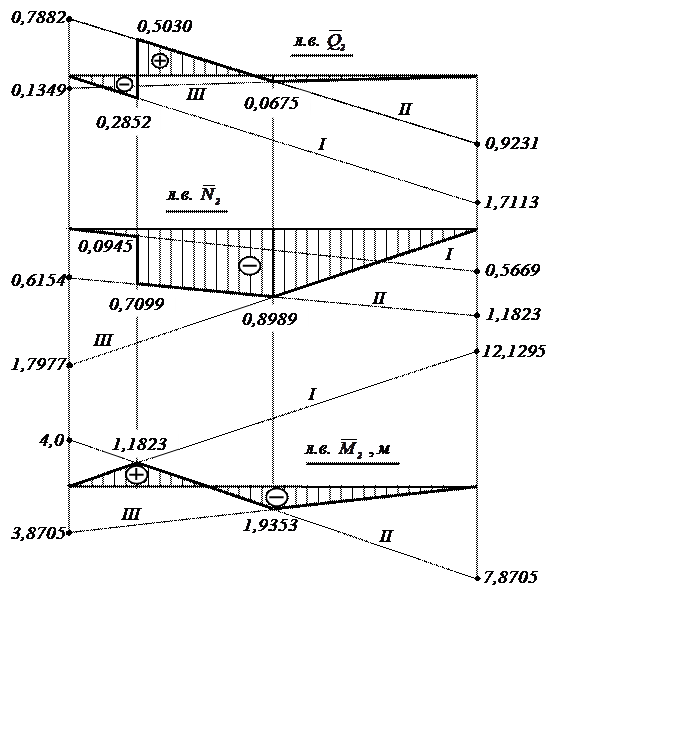
2.6. Строим линии влияния в сечении 9
Линии влияния внутренних усилий в сечении 9 (рис.10, 11, 12) построим, суммируя «скорректированные» балочные линии влияния.
|
|
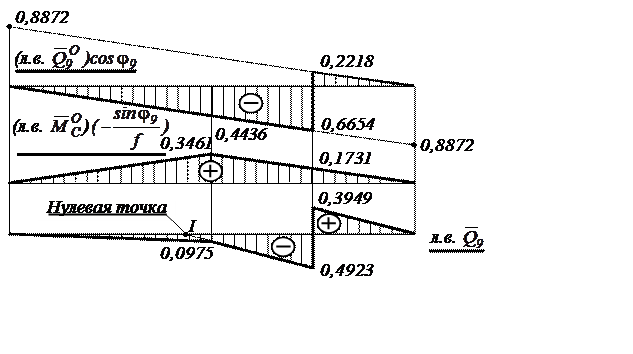
Рис.10
Рис.11
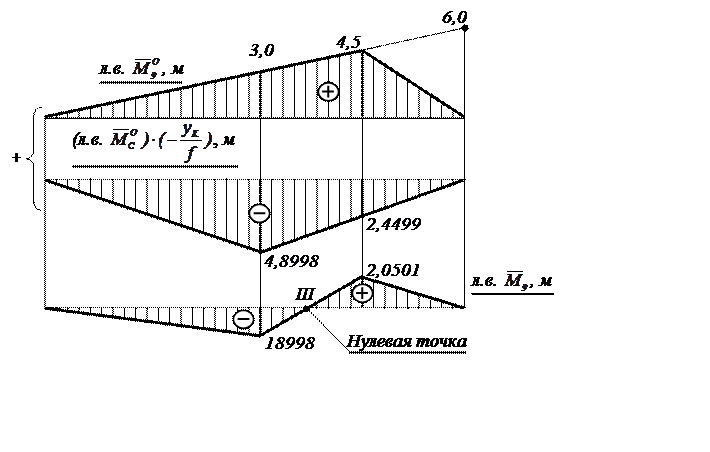
Рис.12
Покажем, что те же значения линий влияния 
на границах участков А–С, С–9, 9–В
можно получить, рассматривая загружение арки единичной силой над шарниром С и
над сечением 9 (рис. 13).
Рис.13
Из рис. 13,а следует, что
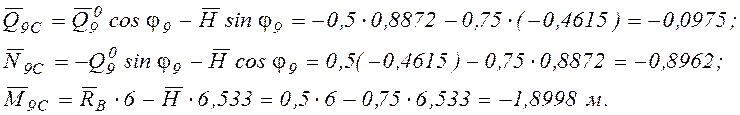
Из рис. 13.б получим
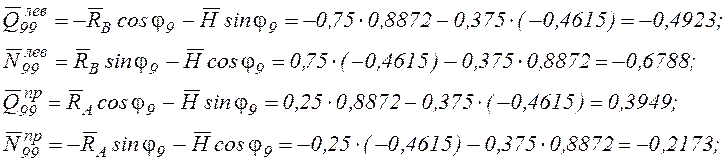
Значения
реакций 
и распора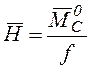 
взяты
с балочных линий влияния (см. рис. 3) при l=24 м; f=8
м; а9=18 м; b9=6
м.
Построение линий влияния рекомендуется проверить, графически определив положение на них нулевых точек. Нулевые точки соответствуют положению единичной силы на арке, при котором исследуемые усилия равны нулю.
В основе графического решения задачи лежит известная из курса теоретической механики теорема о равновесии трёх сил, согласно которой линии действия трёх сил, находящихся в равновесии, пересекаются в одной точке.
Вполне естественно, что графическое решение даст правильный результат только в случае строгого соблюдения масштаба при изображении расчётной схемы арки и тщательном исполнении всех построений.
Приводим
графическое определение нулевых точек линий влияния 
(рис. 14).
Следует
заметить, что при указанных направлениях векторов реакций 
и 
единичная
сила 
должна быть приложена к арке на участке С–9.
Для случаев
и 
это
можно сделать, если воспользоваться консолью, жёстко соединенной с аркой на участке
С–9, т.е. на ветвях линий влияния 
и 
«реальных» нулевых точек нет, они находятся
на продолжении ветвей участка С–9.
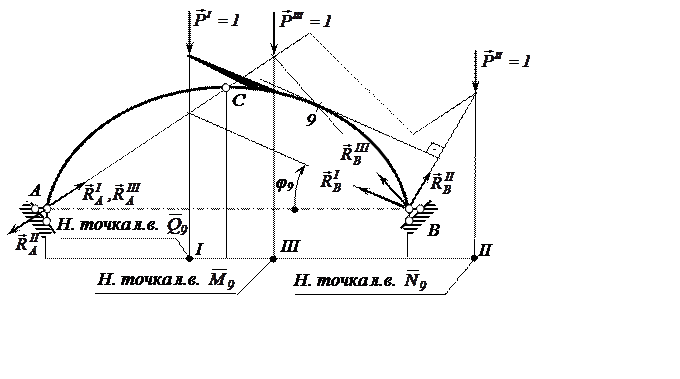
Рис. 14
2.7. Загружаем линии влияния внутренних усилий в сечении 9.
Расположим
линии влияния 
и 
под
схемой нагрузки
(рис. 15).
Напомним правило загружения линий влияния сосредоточенными силами и равномерно распределенной нагрузкой.
.
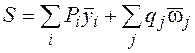Здесь:
S– усилие,
вычисляемое по линии влияния 
;
– сосредоточенные силы;
– интенсивность
распределенной нагрузки;
– значение л.в. под силой Pi;
– площадь л.в. под распределенной нагрузкой qj.
В соответствии с этим правилом получим
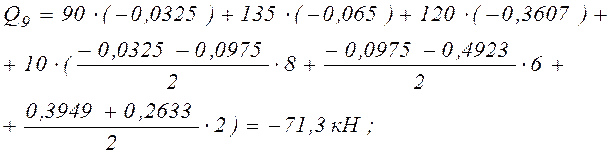
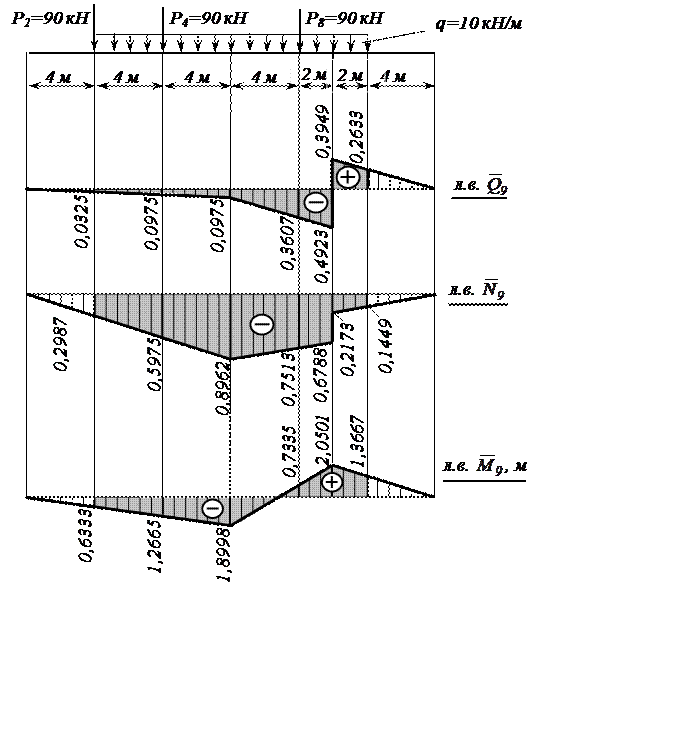
Рис. 15
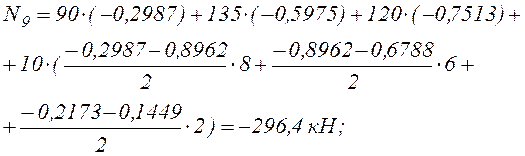
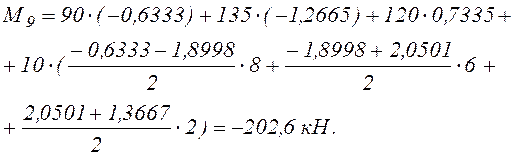
Здесь
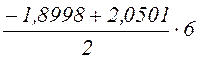– суммарная площадь «перекрученной»
трапеции л.в. 
на участке С–9.
Те же значения Q9, N9, M9 получены при построении эпюр внутренних усилий в арке (см. табл.2).
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Дарков, А.В. Строительная механика: учебник для вузов / А.В. Дарков,
Н.Н. Шапошников. –9-е изд., испр. – СПб. Лань, 2004. – 655 с.
2. Руководство к практическим занятиям по курсу строительной механики: Статика стержневых систем. учеб. пособие для строит спец. вузов / Под общ. ред. Г.К. Клейна. – 4-е изд., перераб. и доп. – М.: Высш. школа, 1980, – 384 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
-301,3