Расчет статически определимых арок: Методические указания к контрольной работе по дисциплине "Строительная механика", страница 2

Аналогично можно вычислить характерные значения линий влияния внутренних усилий в сечении К₂, расположенном справа от шарнира С, учитывая при этом, что

В заключение отметим другой способ вычислений характерных значений линий влияния, изложенный в [1], который основан на определении положения так называемых нулевых точек линии влияния.

2. ПРИМЕР РАСЧЁТА ТРЁХШАРНИРНОЙ АРКИ

Для трёхшарнирной арки, очерченной дугой окружности, расчётная схема которой представлена на рис. 6, требуется:

а) построить эпюры внутренних усилий;

б) построить линии влияния внутренних усилий в сечениях 2 и 9, используя различные способы;

в) загрузить линии влияния в сечении 9 заданной нагрузкой, результаты загружения сравнить со значениями на эпюрах внутренних усилий.

Решение задачи выполняем в такой последовательности.

2.1. Определяем реакции опор и строим эпюры поперечных сил и изгибающих моментов в заменяющей балке (рис. 7).

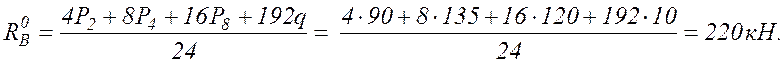
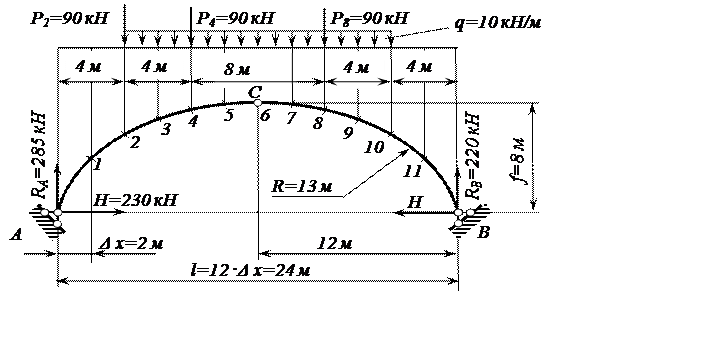
Рис. 6

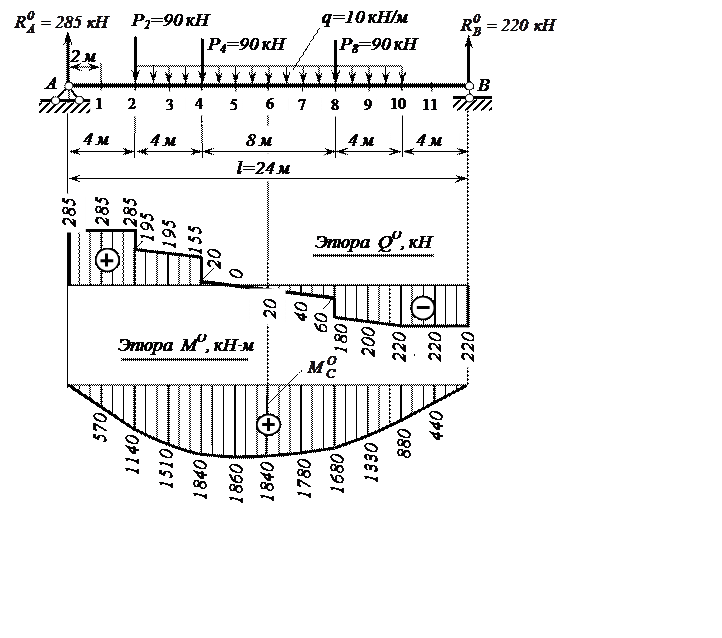
Рис. 7

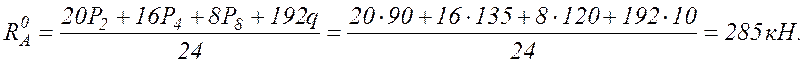Проверка:

т.е. реакции определены правильно.

Эпюру поперечных сил построим по «скачкам» под сосредоточенными силами, начиная с , и «спускам» на участках с равномерно распределённой нагрузкой q на величину равнодействующей.

Эпюру изгибающих моментов M⁰ построим, используя интегральную зависимость

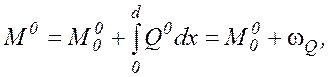
где – изгибающий момент в конце рассматриваемого участка; d – длина участка;  – изгибающий момент в начале участка;  – площадь эпюры поперечных сил на участке.

Эпюры  и  можно построить по значениям внутренних усилий в обозначенных сечениях балки, используя непосредственно метод сечений. Так, например, для сечения 6 (под шарниром С) получим:

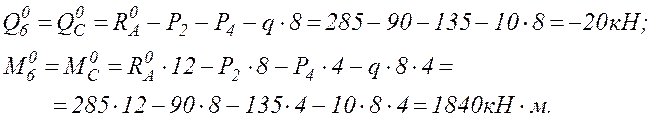
2.2. Определяем реакции опор арки

Вертикальные составляющие

Распор    

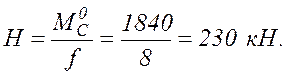
2.3. Вычисляем геометрические параметры арки, входящие в выражения внутренних усилий (2).

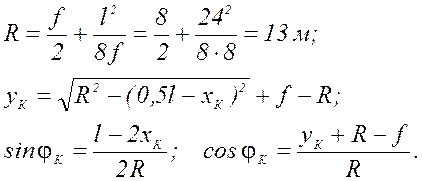
 вычислим для тринадцати сечений, взятых с интервалом . Результаты расчётов сведём в табл. 1.

Таблица 1

Геометрические параметры арки

Номер сечения	х, м	у, м	sin φ	cos φ
А	0	0	0,9231	0,3846
1	2	3,307	0,7692	0,6390
2	4	5,247	0,6154	0,7882
3	6	6,533	0,4615	0,8871
4	8	7,369	0,3077	0.9515
5	10	7,845	0,1538	0,9881
6	12	8,0	0	1,0
7	14	7,845	-0,1538	0,9881
8	16	7,369	-0,3077	0,9515
9	18	6,533	-0,4615	0,8871
10	20	5,247	-0,6154	0,7882
11	22	3,307	-0,7692	0,6390
В	24	0	-0,9231	0,3848

2.4. Строим эпюры внутренних усилий в арке.

Внутренние усилия в каждом из обозначенных сечений вычисляем по формулам ( 2 ). Значения балочных внутренних усилий и берём с эпюр (см. рис. 7), а геометрические параметры арки – из табл. 1.

Заметим, что на эпюрах Q, N под сосредоточенными силами будут «скачки», поэтому при  необходимо рассматривать по два сечения – расположенные чуть левее и чуть правее сечений 2, 4 и 8.

Расчёт M, Q, N сводим в табл. 2.

Эпюры M, Q,N, построенные по значениям в ряде сечений и уточнённые по дифференциальной зависимости между Q и М, изображены на рис. 8.

Эпюра изгибающих моментов должна отвечать дифференциальной зависимости 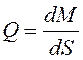 (S – дуга оси арки), т.е. под сосредоточенными силами она «проламывается» в направлении силы, а в сечениях, где  изгибающий момент имеет экстремальные значения.

Эпюры внутренних усилий для криволинейных стержней обычно строят на их осях, однако с целью упрощения построений эпюры для арок принято строить на горизонтальной базовой линии, тем более что и внешняя нагрузка q отнесена к горизонтальному уровню.

Таблица 2

Расчёт внутренних усилий в арке