Определение собственных частот и форм колебаний цепной системы

Определение собственных частот и форм колебаний цепной системы:

Для системы, изображенной на рис.1 составим алгоритм нахождения собственных частот и форм колебаний в программе MathCAD

Для начала зададимся параметрами системы через оператов присвоения (:=)

Определим величину, обратную динамической жесткости, называемую динамической податливостью системы:

Запишем уравнения движения трехмассной цепной системы:

Воспользуемся подстановкой:

Получим систему алгебраических уравнений:

Составим определитель, состоящий из коэффициентов алгебраических уравнений:

Получаем частотное уравнение:

Сделаем замену для определения квадратов частот:

Решая это кубическое уравнение, воспользуемся меню Symbolics, которое содержит команды управления символьным процессом. Для этого поставим курсор возле искомого параметра l, в меню выберем команду Symbolics-Variable-Solve (Символика-Переменная-Решить). На экране появится матрица-стобец, элементы которой будут представлять собой решения кубического уравнения.

Подставим действительные корни частотного уравнения в полученные алгебраические уравнения:

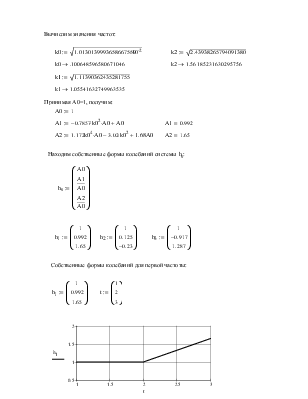
Вычислим значения частот:

Принимая А0=1, получим:

Находим собственные формы колебаний системы :

Собственные формы колебаний для первой частоты:

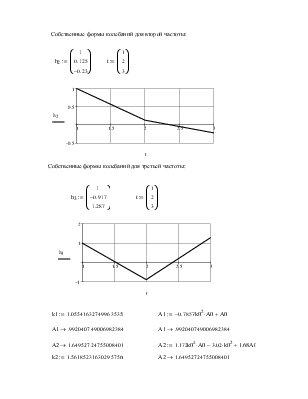
Собственные формы колебаний для второй частоты:

Собственные формы колебаний для третьей частоты: