
Цель нашей работы исследовать влияние глубины водоема на напряжено-деформированное состояние ледяного покрова, находящегося под действием подвижной нагрузки.
Для исследования мы взяли глубину водоема от 5 до 30 метров, с шагом в 5 метров.
Произведя вычисления посредством программы «CRACK» мы находим максимальный прогиб, напряжения по Х и У. Данные заносим в таблицу 1:
|
статика |
5метров |
10метров |
15 метров |
20 метров |
25 метров |
30 метров |
|
|
прогиб |
-0.030633 |
-0.032019 |
-0.030437 |
-0.029912 |
-0.029799 |
-0.02949 |
-0.029705 |
|
напряжение Х |
2.5862e+005 |
1.551e+005 |
1.2139e+005 |
1.1276e+005 |
1.1039e+005 |
1.0896e+005 |
1.0829e+005 |
|
напряжение У |
2.5879e+005 |
4.5842e+005 |
4.5599e+005 |
4.5589e+005 |
4.5497e+005 |
4.554e+005 |
4.5547e+005 |
Для построения графиков прогиба, напряжения по Х и У разделим полученные данные на значения статики. Данные также занесем в таблицу:
|
статика |
5метров |
10метров |
15 метров |
20 метров |
25 метров |
30 метров |
|
|
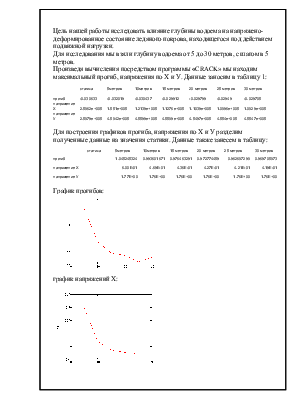
прогиб |
1,045245324 |
0,993601671 |
0,976463291 |
0,972774459 |
0,962687298 |
0,969705873 |
|
|
напряжение Х |
6,00E-01 |
4,69E-01 |
4,36E-01 |
4,27E-01 |
4,21E-01 |
4,19E-01 |
|
|
напряжение У |
1,77E+00 |
1,76E+00 |
1,76E+00 |
1,76E+00 |
1,76E+00 |
1,76E+00 |
График прогибов:
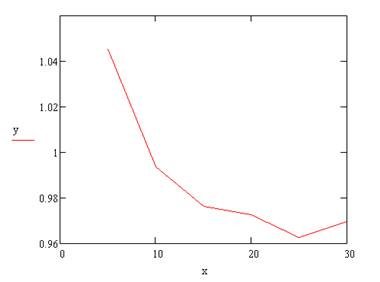
график напряжений Х:
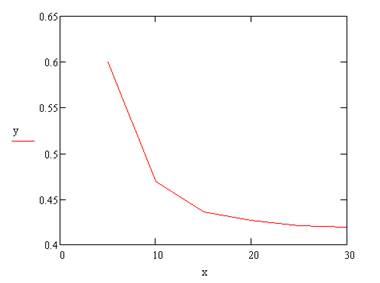
График напряжений У:
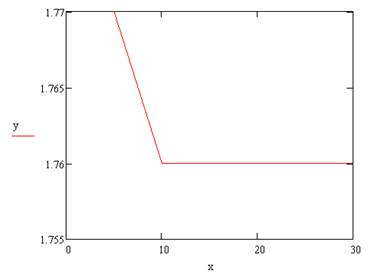
После, мы строим график эквивалентных напряжений. Используем четвертую гипотезу прочности:
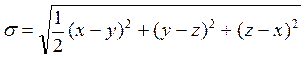
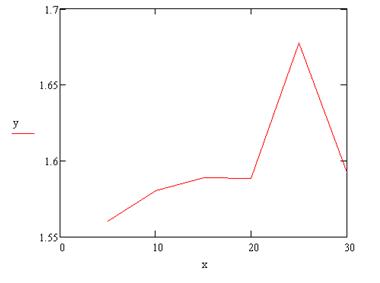
В нашем случае z=0. Данные для построения представлены в таблице:
|
экв.напряжение |
1,560503196 |
1,580487655 |
1,589129706 |
1,588261474 |
1,677705767 |
1,592473606 |
График имеет вид:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.