Поиск рационального класса функции из определённого набора

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Омский Государственный Технический Университет

Кафедра: ЭСПП

Лабораторная работа №5

«Поиск рационального класса функции из определённого набора»

                                                                                    Выполнил: ст-т гр. Э-513

                                                                                                        Матвиец С.В.

                                                                                    Проверил: преподаватель

                                                                                                       Зиновьев М.Е.

Омск 2007

Цель работы: для заданных точек найти рациональную функцию аппроксимации.

Краткая теория.

Всего классов функции 7:

1.  Линейная функция (y=ax+b)

2.  Показательная функция (y=ab^x)

3.  Дробно – рациональная функция ()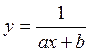

4.  Логарифмическая функция (y=a*ln(x)+b)

5.  Степенная функция (y=ax^b)

6.  Гиперболическая функция ()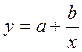

7.  Дробно – рациональная функция ()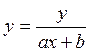

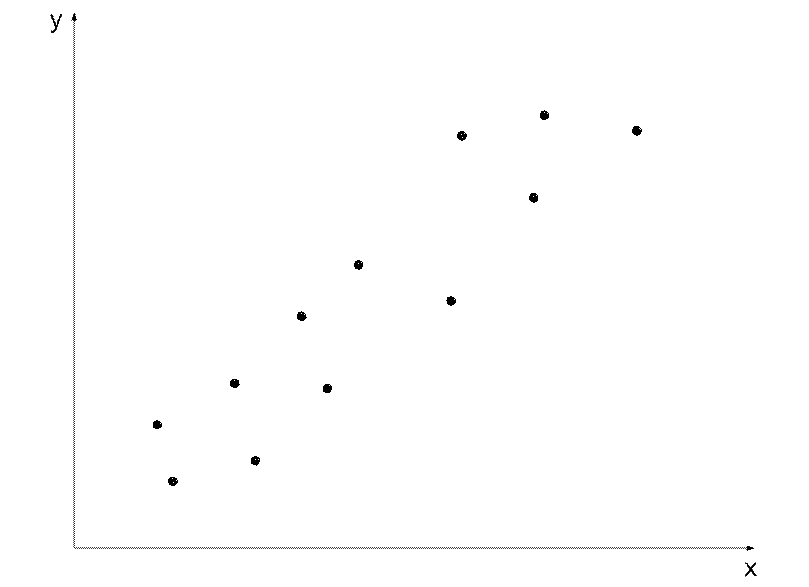
Пусть существует n – точек Х₁,…..,Х_n. Для поиска рациональной функции аппроксимации мы должны найти следующие значения X,Y:

·  среднее арифметическое

·  среднее геометрическое

·  среднее гармоническое

Расчёт будем вести по формулам:

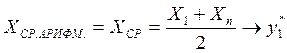
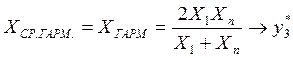
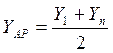
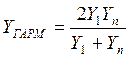
После расчёта найдём невязки по формулам:

В формулах - любые числа.

После расчёта невязок выбираем минимальную невязку, номер минимальной невязки указывает номер функции, которая подходит для аппроксимации.

Задание.

Найти удобную функцию для аппроксимации заданных точек:

хi=	1	yi=	521
	2		308
	3		240
	4		204
	5		183
	6		171
	7		159
	8		152
	9		147

Текст программы.

INPUT "N=" N

INPUT "Y1" Y1

INPUT "Y2" Y2

INPUT "Y3" Y3                                         

DIM X(N),Y(N)

FOR I=1 TO N

INPUT X(I),Y(I)

NEXT I

Xcp=(X(1)+X(N))/2

Xgeom=SQR(X(1)*X(N))

Xgarm=(2*X(1)*X(N))/(X(1)+X(N))

Ycp=(Y(1)+Y(N))/2

Ygeom=SQR(Y(1)*Y(N))

Ygarm=(2*Y(1)*Y(N))/(Y(1)+Y(N))

E1=ABS(Y1-Ycp)

E2=ABS(Y1-Ygeom)

E3=ABS(Y1-Ygarm)

E4=ABS(Y2-Ycp)

E5=ABS(Y2-Ygeom)

E6=ABS(Y3-Ycp)

E7=ABS(Y3-Ygarm)

PRINT "E1=" E1

PRINT "E2=" E2

PRINT "E3=" E3

PRINT "E4=" E4

PRINT "E5=" E5

PRINT "E6=" E6

PRINT "E7=" E7

Результаты расчёта.

Получаем следующий набор невязок:

E1= 151

E2= 93,74356079101562

E3= 46,30239868164062

E4= 94

E5= 36,74356079101562

E6= 7

E7= 111,6976013183594

8.  6 – ая невязка наименьшая, следовательно наилучшая функция

аппроксимации заданных точек – гиперболическая функция ()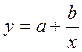

Контрольные расчёты на калькуляторе.

                                             

                                     

                                     

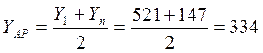
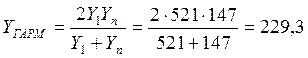
После расчёта найдём невязки по формулам:

  Вывод: В ходе данной лабораторной работы . Проверка расчётов на калькуляторе подтвердила правильность выполненного расчёта.