Построение аппроксимирующей параболы методом средних

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Омский Государственный Технический Университет

Кафедра: ЭСПП

Лабораторная работа №3

«Построение параболы методом средних»

                                                                                    Выполнил: ст-т гр. Э-513

                                                                                                        Матвиец С.В.

                                                                                    Проверил: преподаватель

                                                                                                       Зиновьев М.Е.

Омск 2007

Цель работы: построение аппроксимирующей параболы методом средних.

Краткая теория.

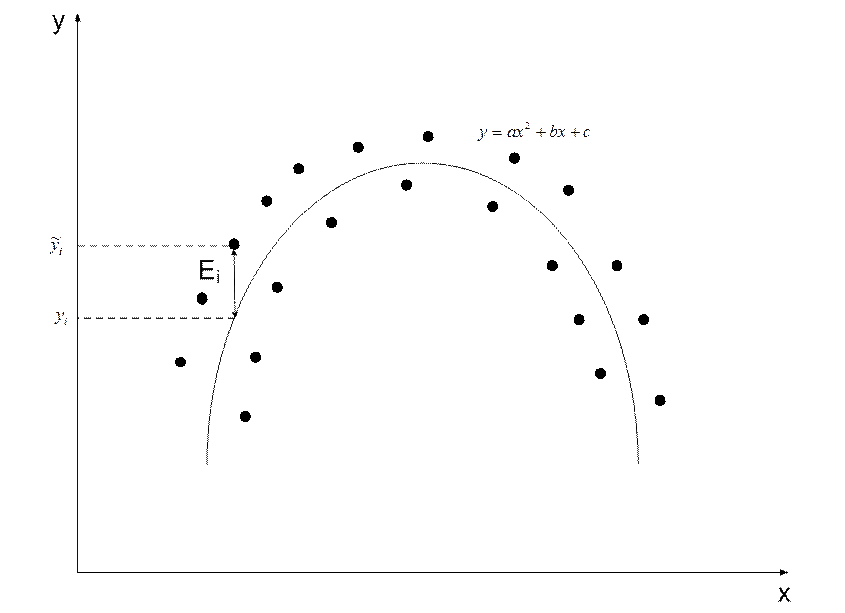
Критерий средних.

Сумма невязок должна быть равна нулю, т.е.

.

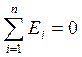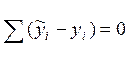  - метод средних

Применительно к функции y=ax²+bx+c, имеем:

 

 

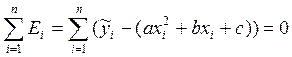
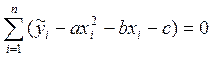
Поскольку интервала три, получаем систему уравнений:

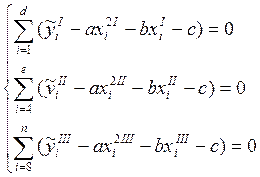
Произведём замену в этой системе уравнений

; ;

; ;

; ;

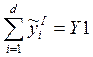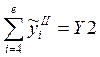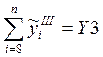
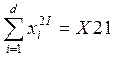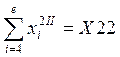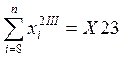
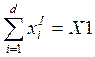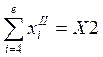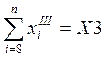
С учётом обозначений получим:

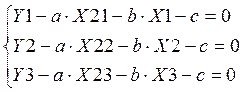
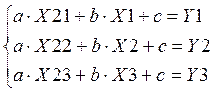
Составим главный определитель системы:

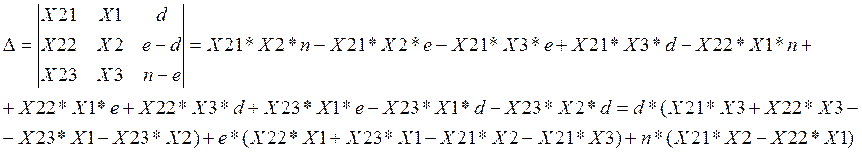
Составим определители ∆₁, ∆₂,  ∆₃ заменой 1-го, 2-го, 3-го столбца на столбец из свободных членов:

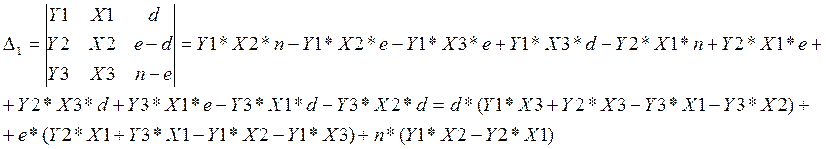
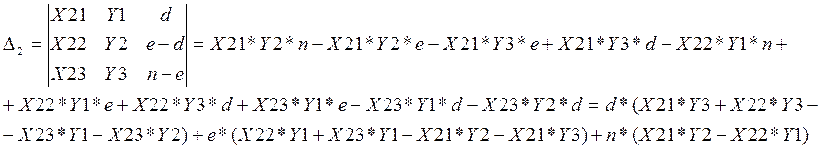
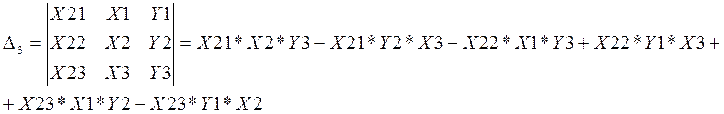
Далее найдём неизвестные коэффициенты a,b,c по следующим формулам:

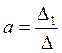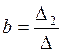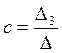; ; , т.е.

Задание (вариант №4).

Построить аппроксимирующую параболу (найти коэффициенты а,b,с) для заданных точек:

xi=	-6	yi=	35
	-6		25
	-4		18
	-1		2
	1		0
	3		0
	4		25
	6		37
	9		75
	10		100

Текст программы.

INPUT "D="D

INPUT "E="E

INPUT N

DIM X(N),Y(N)

FOR I=1 TO N

INPUT X(I),Y(I)

NEXT I

X1=0

X2=0

X3=0

X21=0

X22=0

X23=0

Y1=0

Y2=0

Y3=0

FOR I=1 TO D

Y1=Y1+Y(I)

X21=X21+X(I)*X(I)

X1=X1+X(I)

NEXT I

FOR I=4 TO E

X22=X22+X(I)*X(I)

X2=X2+X(I)

NEXT I

FOR I=8 TO N

Y3=Y3+Y(I)

X23=X23+X(I)*X(I)

X3=X3+X(I)

NEXT I

A=(D*(Y1*X3+Y2*X3-Y3*X1-Y3*X2)+E*(Y2*X1+Y3*X1-Y1*X2-Y1*X3)+N*(Y1*X2-Y2*X1))/(D*(X21*X3+X22*X3-X23*X1-X23*X2)+E*(X22*X1+X23*X1-X21*X2-X21*X3)+N*(X21*X2-X22*X1))

B=(D*(X21*Y3+X22*Y3-X23*Y1-X23*Y2)+E*(X22*Y1+X23*Y1-X21*Y2-X21*Y3)+N*(X21*Y2-X22*Y1))/ (D*(X21*X3+X22*X3-X23*X1-X23*X2)+E*(X22*X1+X23*X1-X21*X2-X21*X3)+N*(X21*X2-X22*X1))

C=(X21*X2*Y3-X21*Y2*X3-X22*X1*Y3+X22*Y1*X3+X23*X1*Y2-X23*Y1*X2)/(D*(X21*X3+X22*X3-X23*X1-X23*X2)+E*(X22*X1+X23*X1-X21*X2-X21*X3)+N*(X21*X2-X22*X1))

PRINT A

PRINT B

PRINT C

END

Результаты расчёта.

a=0,9449628591537476;        b=0,2951168715953827; c=-0,1449538022279739

Контрольные расчёты на калькуляторе.

; ;

; ;

; ;

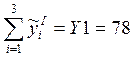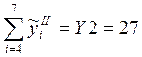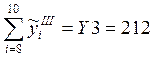
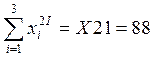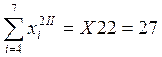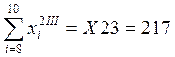
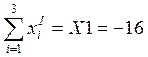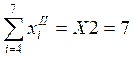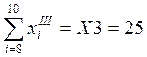
D=3, E=7, N=10

Полученные значения подставим в выражения для a,b,c:

Расчёты проведём в Microsoft Excel. В результате получим значения a,b,c:

a=0,944963

b=0,29466

c=-0,14495

  Вывод: В ходе данной лабораторной работы был окончательно усвоен данный метод аппроксимации (метод средних), поскольку в данной работе была исследована более сложная функция(y(x)=ax²+bx+c). Проверка расчётов на калькуляторе подтвердила правильность выполненного расчёта.