Аппроксимация линейной функции методом средних

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Омский Государственный Технический Университет

Кафедра: ЭСПП

Лабораторная работа №1

«Аппроксимация линейной функции методом средних»

                                                                                    Выполнил: ст-т гр. Э-513

                                                                                                        Матвиец С.В.

                                                                                    Проверил: преподаватель

                                                                                                       Зиновьев М.Е.

Омск 2007

Цель работы: изучить на практике метод линейной аппроксимации, используя критерий средних.

Краткая теория.

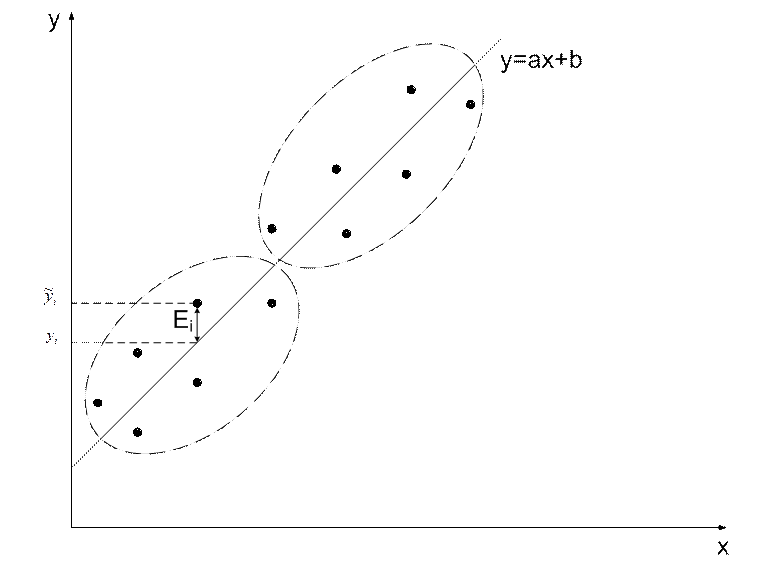
Пусть дана функция y=f(x): y(x)=a₀+a₁x+a₂x²+……..

n=m – число точек(степень полинома)

Аппроксимация – для данной функции f(x) многочлен, принимающий в заданных точках X_i те же значения Y_i ,что и функция f(x), т.е. φ(X_i)=Y_i , i=0,1,……n называется интерполяционным многочленом. Точки X_i – это узлы интерполяции. Максимальная степень полинома m=n говорит о глобальной интерполяции, т.е. один многочлен используется для интерполяции функции f(x) на всём рассматриваемом интервале изменения Х.

Когда интерполяционный полином строится для некоторого интервала изменения Х, говорят о локальной (кусочной) интерполяции.

Экстраполяция – когда интерполяционные многочлены используются для аппроксимации функции вне интервала, ограниченного крайними узлами интерполяции, такой метод называется экстраполяцией.

Критерий средних.

Сумма невязок должна быть равна нулю, т.е.

.

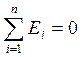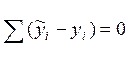  - метод средних

Применительно к функции y=ax+b, имеем:

 

 

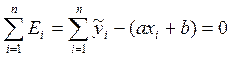
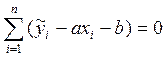
Поскольку интервала два, получаем систему уравнений:

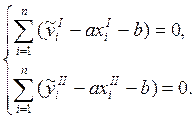
Уравнения можно записать в виде:

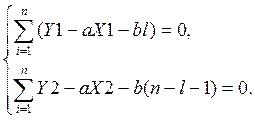
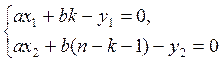
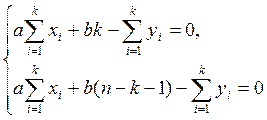
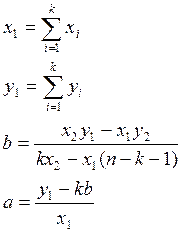
Задание (вариант №4).

Построить аппроксимирующую прямую (найти коэффициенты а и b) для заданных точек:

xi=	-6	yi=	-5
	-6		-5
	-4		-3
	-1		0
	1		2
	3		5
	4		7
	6		8
	9		8
	10		10

Текст программы на языке Turbo Basic

INPUT N

DIM X(N), Y(N)

FOR I=1 TO N

INPUT X(I), Y(I)

NEXT  I 

X1=0

Y1=0

X2=0

Y2=0

K=INT(N/2)

FOR  I=1  TO  K

X1=X1+X(I)

Y1=Y1+Y(I)

NEXT  I 

FOR  I=K+1  TO  N

X2=X2+X(I)

Y2=Y2+Y(I)

NEXT  I

B=(X2*Y1-X1*Y2)/(K*X2-X1*(N-K-1))

A=(Y1-K*B)/X1

PRINT A

PRINT B

END

Результаты расчёта.

a=1.044642925262451;        b=1.142857193946838.

Контрольные расчёты на калькуляторе.

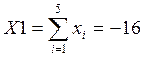
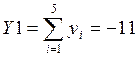
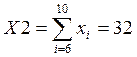
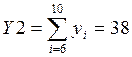
Подставим полученные значения в формулу, т.о. получим:

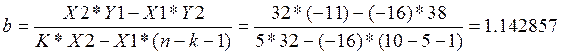
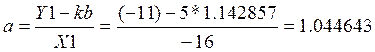
Расчёт на калькуляторе полностью подтверждает правильность полученных результатов.

  Вывод:В ходе выполнения данной лабораторной работы я изучил основы программирования на языке Basic. Проверка расчётов на калькуляторе подтвердила правильность выполненного задания.