Задача №2.
Расчет вероятности зазора и натяга в переходной посадке.
1. Для заданной переходной посадки рассчитать вероятность получения зазоров и натягов. Начертить кривую нормального распределения с графическим определением вероятности.
2. Дать схему расположения полей допусков с указанием предельных зазоров и натягов.
3. Сравнить расчетные и вероятные максимальные зазоры и натяги.
Исходные данные.
Соединением с переходной посадкой в задании является сопряжение ступицы червячного колеса с валом Ø80 Н6/j5.
Решение:
1. По заданной посадке из таблиц СТ СЭВ 144-75 (ГОСТ25347-82) определяем предельные отклонения и рассчитываем предельные и средние зазоры (или натяги), а так же допуски вала и отверстия:
ES= + 19 мкм; EI = 0; es = +6 мкм; ei = -7 мкм .
Smax= ES - ei = 19 – (-7) = 26 мкм
Smin= EI – es = 0 – 6 = - 6 мкм, т.к. зазор отрицательным быть
не может, то Nmax= 6 мкм.
Sm= (Smax+ Smin)/2 = (26 + (-6))/2 = 10 мкм; Sm= 6,5 мкм
TD= ES – EI = 19 – 0 = 19 мкм.
Td= es – ei = 6 –(-7) = 13 мкм.
2. Определяем среднее квадратичное отклонение размеров вала, отверстия и посадки:
sD = TD/6 = 19/6 = 3,17 мкм.
sd = Td/6 = 13/6 = 2,17 мкм
![]()
![]() sS = √sD2 + sd2 = √ 3,172 + 2,172 = 3,842 мкм.
sS = √sD2 + sd2 = √ 3,172 + 2,172 = 3,842 мкм.
3. Определяем предел интегрирования:
Z = Sm/sS = 10/3,842 = 2,6
4. По значению Z определяем функцию Ф(Z) [1, прил.4]:
Ф(Z = 0,6) = 0,4953
5. Рассчитываем вероятность и процент зазора:
р(S) = 0,5 + Ф(Z) = 0,5 + 0,4953 = 0,9953
P(S) = р(S) x 100% = 0,9953 х 100% = 99,53%
6. Рассчитываем вероятность и процент зазора:
р(N) = 0,5 - Ф(Z) = 0,5 - 0,4953 = 0,0047
P(N) = р(N) x 100% = 0,0047 х 100% = 00,47%
7. Определяем значения вероятностных максимальных зазора и натяга:
Spmax=3sS + Sm = 3 x 3,842 + 10 = 21,5 мкм.
Npmax = 3sS - Sm = 3 x 10,7251 - 10 = 1,5 мкм.
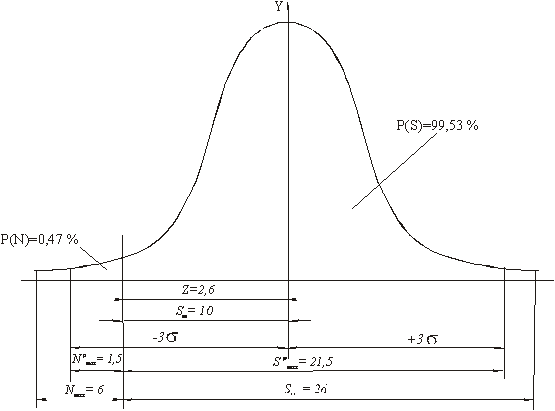
Рисунок 2. Кривая нормального распределения для определения вероятности зазоров и натягов посадки червячного зубчатого колеса на вал.
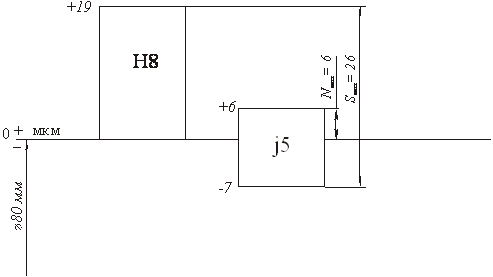
Рисунок 3. Схема расположения полей допусков посадки Ø80 Н6/j5.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.