Информатика и выч. техника \ Автоматизация принятия управленческих решений

Принятие управленческих решений с использованием статистического метода управления и приемов корреляционно-регрессионного анализа, страница 4

σY

σX1

σX2

σX3

σX4

σX5

cov(X1,Y)

cov(X2,Y)

cov(X3,Y)

cov(X4,Y)

6,95

3,45

0,33

1,57

1,85

2,99

13,88

1,52

8,40

7,87

cov(X5,Y)

cov(X1,X2)

cov(X1,X3)

cov(X1,X4)

cov(X1,X5)

cov(X2,X3)

cov(X2,X4)

cov(X2,X5)

cov(X3,X4)

cov(X3,X5)

cov(X4,X5)

13,59

1,03

0,83

-0,29

10,03

0,16

0,11

0,93

2,40

1,21

0,29

Расчёт коэффициентов парной корреляции.

R(Y,X1)

R(Y,X2)

R(Y,X3)

R(Y,X4)

R(Y,X5)

R(X1,X2)

R(X1,X3)

R(X1,X4)

0,58

0,67

0,77

0,61

0,66

0,92

0,15

-0,05

R(X1,X5)

R(X2,X3)

R(X2,X4)

R(X2,X5)

R(X3,X4)

R(X3,X5)

R(X4,X5)

0,97

0,30

0,18

0,96

0,83

0,26

0,05

В результате формируется матрица коэффициентов парной корреляции, которая имеет следующий вид:

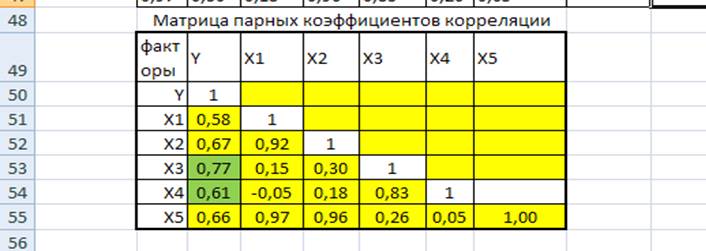
Интерпритация. Значение коэффициентов парной корреляции є (-1;1), его «+» означает прямую связь, «-» говорит об обратной связи. Чем ближе R=│1│, тем теснее связь, она достаточно сильна если R >│0,7│ и слабой если R <│0,4│.

Мультиколлениарность. Многие факторы имеют между собой тесную зависимость. Это явление называется мультиколлениарное. Считается, что это явление в исходных данных установлено, если R между двумя факторами >│0,8│. Чтобы избавиться от мультиколлениарности в модель включают только 1 из линейно связанных факторов, тот, который в большей степени связан с зависимой переменной.

Следовательно, можно сделать вывод, что наибольшее прямое влияние на изменение объёма покупаемых полуфабрикатов оказывают такие факторы как реклама и цена.

Регрессионный анализ. Цель – получение регрессионной модели, т.е. функциональной зависимости результативного показателя Y от значений выбранных факторов. Для отображения зависимостей переменных могут использоваться зависимости многих видов, но в практической работе наибольшее распространение получили модели линейной зависимости, в которой факторы входят в модель линейно.

Построим линейную модель регрессии. Для этого используем инструмент Регрессия: анализ данных →регрессия. Затем заполняются поля диалогового окна регрессии: входной интервал Y – диапазон ячеек зависимой переменной и это всегда один диапазон; входной интервал X – вводятся адреса всех диапазонов, которые содержат значения независимых переменных (max = 16), если при вводе диапазонов выделены заголовки столбцов, то необходимо установить флажок в Метки 1 строки. Необходимо выбирать параметры вывода – Новый лист.

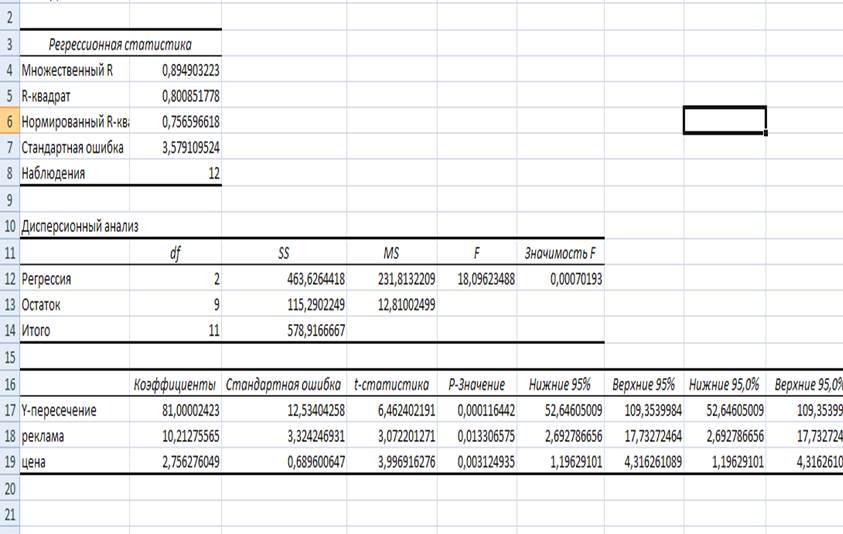
В результате получено уравнение регрессии:

Y = 81+10,21x1+2,76x2;

Проанализируем влияние факторов на зависимую переменную по модели ( для каждого коэффициента регрессии вычислим коэффициент эластичности, ß-коэффициент, ∆- коэффициент).

Скачать файл