Построение линии пересечения поверхностей. Способ вспомогательных сферических поверхностей

МИНИСТЕРСТВО АГРАРНОЙ ПОЛИТИКИ УКРАИНЫ

КЕРЧЕНСКИЙ  ГОСУДАРСТВЕННЫЙ  МОРСКОЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра «Оборудование пищевых и рыбообрабатывающих производств»

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ, ИНЖЕНЕРНАЯ И КОМПЬЮТЕРНАЯ ГРАФИКА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению   контрольных работ

 на тему: «Построение линии пересечения поверхностей.

Способ вспомогательных сферических поверхностей»

для студентов   направлений

6.070104 «Морской  и речной  транспорт»

 специальности «Судовождение»,

«Судовождение и промрыболовство»,

«Эксплуатация судовых энергетических установок»

6.050702  «Электромеханика»,

6.051701 «Пищевые технологии и инженерия»,

6.050503 «Машиностроение»,

дневной  и  заочной  формы обучения    

Керчь, 2009

Составители: Кирсанова В.В., ст. преподаватель кафедры ОПРП  КГМТУ

Рецензент:  Сушков О.Д. к.т.н. доцент, зав. каф. ОПРП

Методические указания рассмотрены и одобрены на заседании кафедры ОПРП  КГМТУ,

протокол № ____ от « _____» _______ 2009  г.

Методические указания рассмотрены и рекомендованы к утверждению  на заседании методической комиссии ТФ  КГМТУ,

протокол №____ от «_____» ________2009  г.

Методические указания утверждены на заседании Методического совета КГМТУ,

Протокол № ______ от «_____» _______2009 г.

© Керченский государственный морской технологический университет

1 Введение

В настоящих методических указаниях рассматривается решение задач с помощью вспомогательных сферических (шаровых) поверхностей. Это, например, задачи 12 и 13 «Методических указаний и контрольных заданий по начертательной геометрии и инженерной графике», по которым выдаются задания студентам – заочникам. Это также  задача к эпюру 4а, выполняемая студентами дневного отделения.

            Задания на контрольные работы индивидуальные. Они представлены в вариантах. Студент заочной формы обучения  выполняет тот вариант задания, номер которого соответствует сумме двух последних цифр шифра зачетной книжки. Вариант студента дневной формы обучения  распределяет преподаватель.

            Работа выполняется на ватмане формата А3,  сдается на кафедру для проверки преподавателем, после чего защищается студентом.

            2 Основные положения

            Поверхности вращения с общей осью вращения называют соосными . Известно замечательное свойство: две любые соосные поверхности вращения (например, изображенные на рисунке 2.1-а,б пересекаются по окружностям, проходящим через точки пересечения меридианов поверхностей (рисунок 2.1-в). Эти окружности – общие параллели поверхностей проецирующиеся в отрезки прямых, если ось вращения параллельна плоскости проекций.

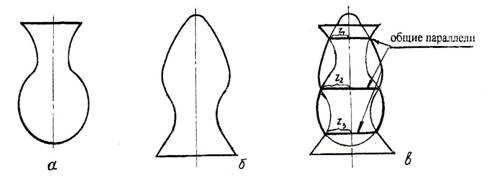
Рисунок 2.1

Сферическую поверхность целесообразно применять в качестве вспомогательной, потому что она проста в изображении и любой диаметр сферы может служить осью вращения. А это значит, что сфера может быть соосной любой поверхности вращения при условии, что центр сферы лежит на оси вращения этой поверхности (рисунок 2.2).

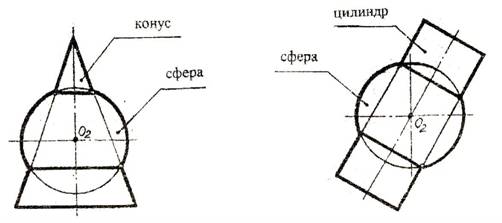
Рисунок 2.2