КЕРЧЕНСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ИНЖЕНЕРНОЙ МЕХАНИКИ
УТВЕРЖДЕНО
На заседании кафедры
Протокол № ________
От __________ 2008 г.
ЛАБОРАТОРНАЯ РАБОТА № 9
по курсу: «СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ»
ОПРЕДЕЛЕНИЕ ПРОГИБОВ
ПРИ КОСОМ ИЗГИБЕ
Керчь 2008г.
Мисько В.В. Лабораторная работа №9 пол курсу «СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ». Методические указания по выполнению лабораторной работы ОПРЕДЕЛЕНИЕ ПРОГИБОВ ПРИ КОСОМ ИЗГИБЕ
Рецензент: Горбенко А.Н., к.т.н., доцент кафедры СЭУ.
Методические указания рассмотрены и одобрены на заседании кафедры инженерной механики КМТИ.
Протокол № 32 от 15.05.1999г.
Методические указания утверждены на ученом совете КМТИ.
Протокол № 11 от «01» июля 1999 г.
1. ЦЕЛЬ РАБОТЫ.
Целью работы является определение опытным путем величины и направления прогиба свободного конца консольной балки при косом изгибе, сравнение опытных данных с теоретическими.
2. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
Изгиб является одним из наиболее распространенных видов деформации упругих систем.
В зависимости от положения силовой плоскости, т.е. от положения продольной плоскости, в которой расположены действующие нагрузки, изгиб бывает плоским или косым.
Если эта плоскость совпадает с одной из главных плоскостей инерции балки, изгиб называется плоским.
Если силовая плоскость не совпадает ни с одной из главных плоскостей инерции балки, то изгиб называется косым. Косой изгиб относится к сложным видам деформации.
Применяя принцип независимости действия сил (принцип
суперпозиции), его рассматривают как сочетание двух плоских изгибов. Поэтому
прогибы ![]() при косом изгибе определяются
геометрическим сложением прогибов в направлении главных осей поперечного
сечения балки.
при косом изгибе определяются
геометрическим сложением прогибов в направлении главных осей поперечного
сечения балки.
![]() ,
,
где:
![]() – прогиб в определяемом сечении по
направлению главной оси
– прогиб в определяемом сечении по
направлению главной оси ![]() ;
;
![]() – то же по направлению главной оси
– то же по направлению главной оси ![]() ;
;
Интегрируя дифференциальные уравнения изогнутой оси балки для консольной балки (рис. 1а) с жестко закрепленными одним концом и приложенной силой на свободном конце, получим прогибы (рис. 1б).
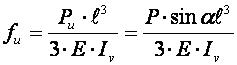 ;
;
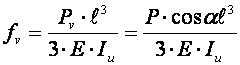 ,
,
где:
![]() и
и
![]() – составляющие силы
– составляющие силы ![]() по направлениям главных осей
по направлениям главных осей ![]() и
и ![]() сечения
балки (рис. 1б).
сечения
балки (рис. 1б).
![]() –
длина консоли (рис.1а);
–
длина консоли (рис.1а);
![]() –
модуль упругости материала балки;
–
модуль упругости материала балки;
![]() и
и
![]() – главные центральные моменты
инерции относительно осей
– главные центральные моменты
инерции относительно осей ![]() и
и ![]() ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.