Определение прогибов при косом изгибе (лабораторная работа), страница 2

 – угол между направлением силы и главной осью  (рис.1б).

Примененный для определения прогибов принцип суперпозиции справедлив, если материал подчиняется закону Гука и деформации малы по сравнению с размерами балки.

Границы применяемости закона Гука на диаграмме растяжений определяются пределом пропорциональности, для напряжения эта величина . Чтобы не превысить этот предел, необходимо вычислить максимально допустимую нагрузку  из условия.

;

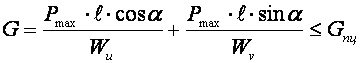Решив это уравнение относительно , получим

,

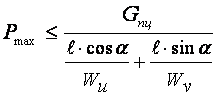где:

 и  – моменты сопротивления поперечного сечения уголка относительно главных осей  и ;

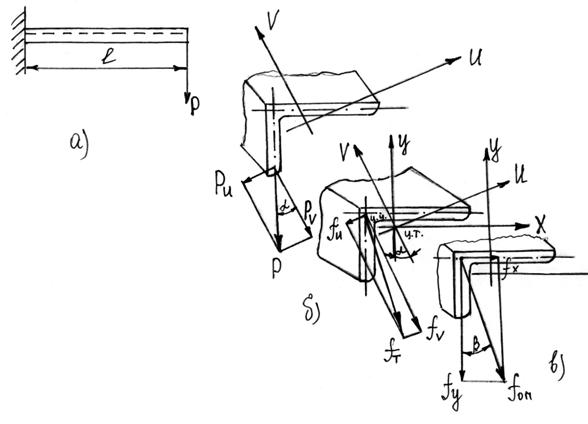
Рис.1 Косой изгиб защемленной балки.

а) схема нагружения балки;

б) деформация  свободного конца балки и ее составляющие по осям  и , а также силы ;

в) Разложение деформации  на составляющие  и .

Если поперечному изгибу подвергается балка не симметричного сечения, то вследствие действия касательных напряжений в сечении, балка может скручиваться этими напряжениями. Для предотвращения этого явления, силу необходимо прикладывать не в ц.т. сечения, а в центре изгиба (ц.и., рис. 1б).

Эта точка находится на пересечении осей полок уголка как равнобокого, так и не равнобокого.

Чтобы получить косой изгиб без кручения для уголкового поперечного сечения, достаточно приложить силы вдоль оси одной из полок (рис.1б). Главные центральные оси  и , наклонены под углом  к осям полок, что равносильно косому изгибу.

При косом изгибе направление полного прогиба не совпадает с силовой плоскостью (рис.1б). По этой причине нейтральная линия не перпендикулярна к силовой плоскости, а несколько отклонена в сторону оси минимального момента инерции.

Для опыта выбирается одна из предложенных ниже балок уголкового поперечного сечения.

Данные материала и сечения для уголковых балок см. таблицу.

Таблица 1.

№ п/п	Параметры	Обозначение	Един. Измер.
1.	Материал			алюминий	алюминий	Сталь
2.	Модуль продольной упругости
3.	Предел пропорциональности
4.	Моменты инерции
5.	Моменты сопротивления
6.	Угол наклона оси