Проектирование ступенчатых колонн, страница 2

Проверим местную устойчивость пояса ветви:

,

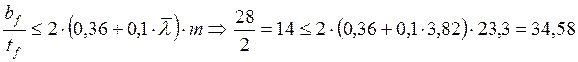следовательно, местная устойчивость пояса ветви обеспечена.

Проверим общую устойчивость ветви:

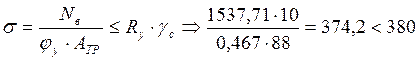МПа

общая устойчивость подкрановой ветви обеспечена.

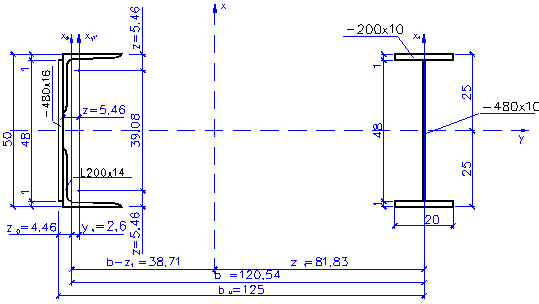
Рисунок 14 – Сечение нижней части сквозной колонны

Наружную ветвь рассчитываем на усилие N_н =1778,43кН. Требуемая площадь ветви:

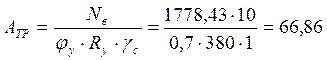см²

Компонуем ветвь из листа 480х16мм и двух уголков 200х14.

Характеристики сечения: см²

Координаты центра тяжести: см;

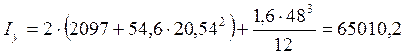тогда см.    см⁴

 см⁴

см              см

Гибкости: 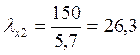 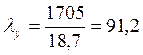                           ;  φ_min=0,464

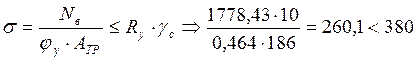МПа

Устойчивость наружной ветви обеспечена.

Ранее приведенные усилия в ветвях определены в предположении, что нейтральная ось проходит посередине сечения, поэтому нормальная сила между ветвями распределялась поровну. Теперь, имея сечение ветвей можно определить точное положение нейтральной оси сечения после чего уточнить усилие в ветвях.

Определим центр тяжести всего сечения:

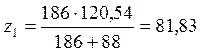см

Корректируем усилия в ветвях:

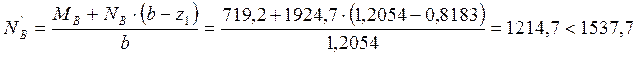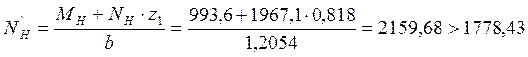кН

кН

Устойчивость наружной ветви проверим повторно:

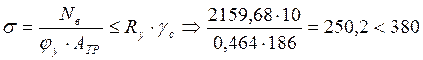МПа

Устойчивость обеспечена.

Геометрические характеристики всего сечения:

см⁴

см⁴

см²     см         см

              ;

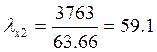
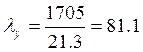Для проверки устойчивости колоны как целого стержня предварительно определяем сечение раскоса, который выполняют из одиночного уголка. Раскосы рассчитываются на большую поперечную силу Q: фактическую или условную Q_fic.

Расчет раскоса производим на большую поперечную силу: расчетную Q=66,5кН или условную определяемую по формуле:

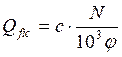, где

c – величина, принимаемая по табл. 9 c=12,8;  N – наибольшая сила в нижней части колонны N=1967,1кН. Коэффициент продольного изгиба определяем по гибкости λ_х=1705/63,66=26,78, откуда φ=0,927, следовательно:

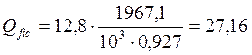кН

Расчетной является сила Q=66,5кН.

Тогда расчетное усилие в раскосе одной системе планок (sinα=0,86)

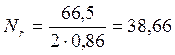кН

Требуемая площадь сечения раскоса при φ=0,7 и =0,75:

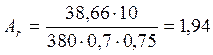см²

Принимаем уголок 63х5; A_r=6,13см²; i_min=1,25см; , откуда φ=0,316

Проверим, обеспечена ли устойчивость раскоса:

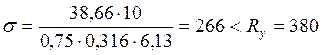МПа

устойчивость раскоса обеспечена.

Устойчивость нижней части колонны как целого стержня в плоскости действия момента поверяем по двум расчетным комбинациям усилий. Вычислим приведенную гибкость колонны по формулам:

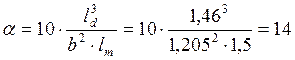
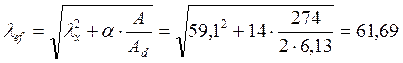
Условная гибкость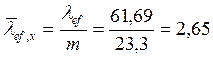

Проверку устойчивости колонны как целого стержня производим в таблице 4.

Таблица 4 – Проверка устойчивости колонны как целого стержня

Формула	Комбинация №1 усилий	Комбинация №2 усилий
N, кН	1924,7	1967,1
M, кН∙м	719,2	993,6
,м	0,374	0,505
, см
	2,65	2,65
(табл. 75 СНиПа)	0,558	0,352
	МПа	МПа

4.3 Расчет верхней части колонны

Расчетными усилиями M и N являются те, которые вызывают наибольшее сжатие крайнего волокна колонны в сечениях C или BC. Эти усилия будут равны: M=573,6кН∙м и N=603,6кН∙м. Требуемую площадь верхней части колонны приближенно устанавливают оп формуле:

,

где φ_х – коэффициент продольного изгиба; , (см, откуда , следовательно φ_х=0,768

Тогда

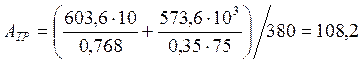см²

Наибольший по абсолютной величине момент на опоре ригеля (таблица машинного расчета) M=619,7кН∙м, при высоте ригеля в осях 3,1м получим перерезывающую силу:

кН

При высоте стенки h_w=75-4=71см толщина стенки определяется из условия прочности на срез по формуле: