Строительные конструкции: Программа, методические указания, задания на контрольную работу и расчетно-графическую работу, страница 20

Расчет выполнять в соответствии со СНиП П-25-80* [5 ] и СНиП 2.01.07-85* [ 1 ]

( в скобках даны номера по списку литературы ).

1. Статический расчет.

1.1.  Расчетная схема стропильной ноги (рис.1 )

1.2.  По классу ответственности и капитальности устанавливаем значение

 коэффи­циента γ _n  =О.95.

1.3.  Устанавливаем коэффициенты надежности для снеговой нагрузки γ _f [1 п. 5.7]

1.4.  Нагрузка на 1 п. м. горизонтальной проекции стропильной ноги

 ;   

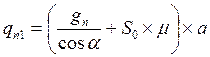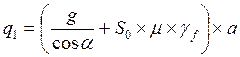
где Sо - вес снегового покрова на 1 м' горизонтальной поверхности земли, принимаемый по [ 1 табл. 4 ] карте № 1 в зависимости от района строительства

μ - коэффициент перехода от веса снегового покрова на земле к снеговой на­грузке на покрытии принимаемый по [ 1. с, 23 приложение 3*]

1.5. Определяем изгибающий момент в сечении над средней опорой

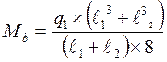
1.6. Длина верхнего и нижнего участка стропильной ноги

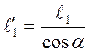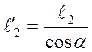       м;

       м

2. Конструктивный расчет.

2.1.Требуемый момент сопротивления стропильной ноги из условия прочности

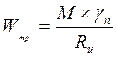 см³,

где  R_u- расчетное сопротивление древесины [5.c.7-9 табл.3 ] с учетом коэффициента условия работы по [5. п.3.2]

2.2.   Определяем сечение стропильной ноги различного типа.

2.2.1. При прямоугольном сечении принимаем h ≈ 2b,  тогда

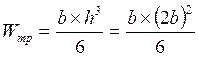 отсюда 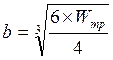,  a      h=2b

2.2.2  Определяем Д бревна в сечении над опорой В.

       см;

расчетный диаметр бревна в сечении на опоре С равен

Д_с=Д⁰+0.008 ∙ ℓ'₂   см , а на опоре А : Д_А=Д⁰-0.008 ∙ ℓ'₁

0.08 м =0.8 см ( сгон – 0.8 см на 1 м длины бревна)

2.2.3 Принятые размеры  уточняем по сортаменту ( приложение 2)

2.3. Проверка прочности подобранного сечения

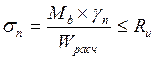      кН/см²

где   W_расч  -расчетный момент сопротивления поперечного сечения элемента. Для цельного элемента.

W_расч  = W_нт

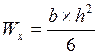      см³  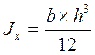 ;     см⁴ ; (для бруса)

для бревна , стесанного сверху на Д/3

W_х=0.096 ∙ Д³ см³; J_x=0.0476 ∙  Д⁴ см⁴

2.4. Проверяем принятое сечение в середине нижнего участка под действием пролетного момента М₁ считая в запас прочности значение момента  как для простой балки на двух опорах длиной ℓ₁

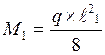     кНм

2.5. Проверка прочности нижней части стропильной ноги

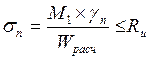       кН/см²

2.6 Проверка жесткости стропильной ноги

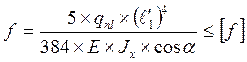
где  Е – модуль упругости древесины Е = 10⁴ МПа =10³ кН/ см²

[f] –   предельные прогибы [1. табл. 19]

3. Выполнить чертежи стропильной системы в масштабе 1:100 , узлов в масштабе 1:20

( приложение 3) . Чертеж оформить надписью по форме [ 13, С. 61]  и рамкой.

8. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЗАДАЧЕ №3.

Задачу решать в соответствии со СНиП II -22-81 [ 4 ].

Рекомендуется следующая последовательность решения задачи:

1.Статический расчет.

1.1. Определить класс здания по степени ответственности и капитальности , установить значение γ_n [ 1 . приложение 7^*]

1.2. Площадь сечения кирпичного столба А= b∙ h  м² в соответствии с требованием [4.с.8 п .3.11.] и примечанием к [ табл. 1,4] устанавливаем значение коэффициента условий работы γ_c1 [4, табл. 1]  (на раствор ), γ_c2

[ 4, п.3.11] . Окончательно устанавливаем сопротивление кладки сжатию с учетом этих коэффициентов     R [4.табл. 1] ,   R∙ γ_c1∙ γ_c2  ( кН/см²)

1.3. Определяем упругую характеристику неармированной кладки α [ 4, с. 12 , табл. 15]

1.4.Гибкость столба в плоскости действия изгибающего момента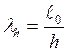  

1.5. По гибкости λ_h и упругой характеристики α  находим коэффициент продольного изгиба φ для всего сечения [4, с. 13 , табл. 18] 

2. Конструктивный расчет.

2.1. Проверка несущей способности внецентренно – сжатого столба

N < m_q ∙ φ ₁∙ R∙A_c ∙ ω  кН

2.1.1. Коэффициент продольного изгиба внецентренно – сжатого элемента

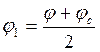
φ_с –коэффициент продольного изгиба сжатой части сечения , определяемый по фактической высоте Н в плоскости действия изгибающего момента , деленный на высоту сжатой части сечения  h_c  [4,с.13 , табл. 18]

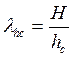;    h_c=h - 2∙℮₀   (см) – для прямоугольного сечения

2.2.2.Коэффициент , учитывающий влияние длительной нагрузки m_g  , при h ≥ 30 см, m_g  [4,с.13 , п.4.1]