Розрахунок даних для перенесення кривої на місцевість, страница 4

Закінчення таблиці 8.6

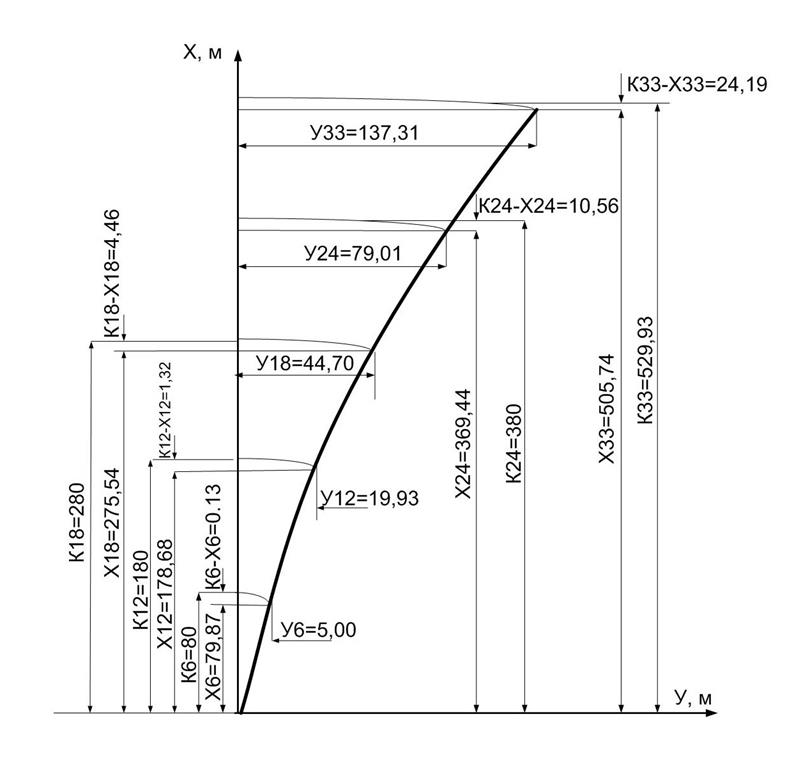
         Рисунок 8.5 - Детальна розбивка кривої способом прямокутних координат

Розбивка кривих по способу прямокутних координат дає найбільш точні результати. Цей спосіб вигідно застосовувати на відкритій рівній місцевості.

8.2.2 Спосіб кутів

Спосіб кутів оснований на тому,що кути з вершиною в будь-якій точці на колі,утворенні дотичною і січною та заключні рівні дуги , рівні між собою і рівні половині центральних кутів.

Із Рис.8.6   видно,що хорда    s =2sinφ/2·R ; Звідси:   sinφ/2 = s/2R

Встановивши в точці А теодоліт, зміщаемо нуль лімба з нулем алідади,візіруємо на точку М і від напрямку АМ обертанням  алідади відкладаємо кут  φ/2 . Відклавши стрічкою по напрямку візірного променя відрізок  s  , отримуємо точку В кривої. Потім обертаємо алідадний круг на кут  2φ/2 (від напрямку АМ).Змістивши початок стрічки з точкою В,протягують її по напрямку візірної вісі труби теодоліта і,відклавши відстань s від точки В,отримуемо точку С кривої і т.д. В точках В,С,D,…  забивають коли.

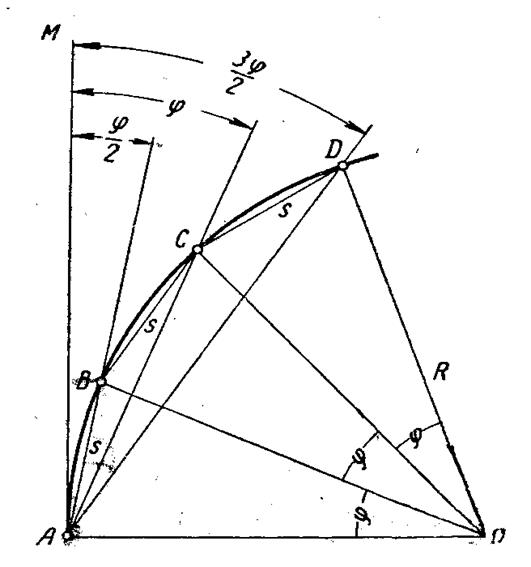
Рисунок 8.6 - Спосіб кутів

 Отже,значення кутів φ для розбивки знаходяться за формулами:

Sinφ=a/(2R);                                                 (8.25)

φ=arcsin a/(2R);                                             (8.26)

де       а – довжина хорди в заданому інтервалі розбивки

           Результати розрахунків заносимо у таблицю 8.7

 Таблиця 8.7 – Розрахунок кутів