Розрахунок даних для перенесення кривої на місцевість, страница 2

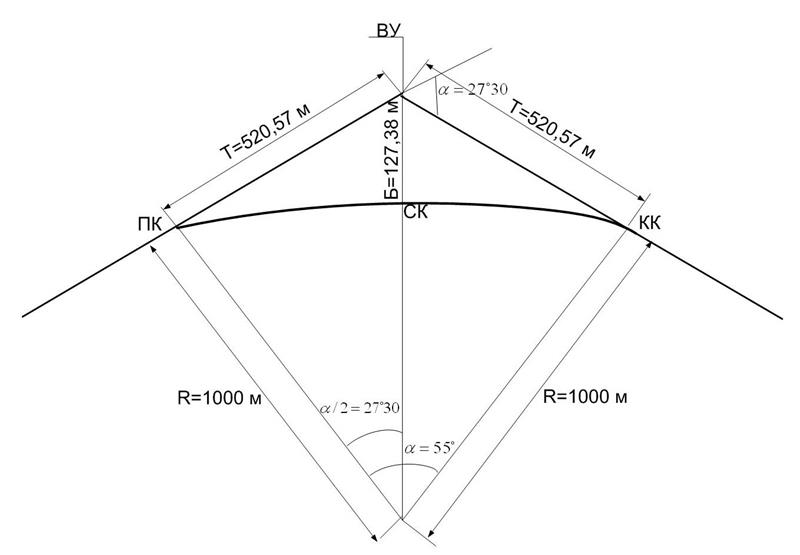
Рисунок 8.2 - Основні елементи і головні точки кривої

 Таблиця 8.3 – Поправки

Таблиця 8.4 – Основні елементи з урахуванням перехідних кривих  

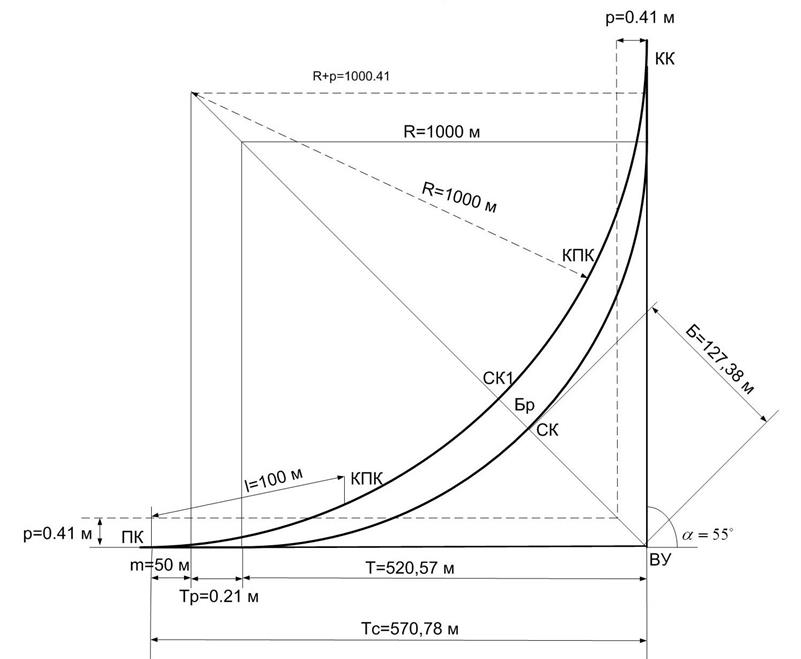
Рисунок 8.3 - Основні елементи кривої з урахуванням поправок

Таблиця 8.5 – Головні точки кривої 

8.2 Детальна розбивка кругової кривої

При будівництві залізничної лінії на місцевості криві потрібно позначити через порівняно невеликі інтервали для того що б дугу кривої в цих інтервалах практично можна було б приймати за прямий відрізок.На практиці ці інтервали знаходяться в межах  від 5 до 40м,в залежності від радіуса кривої.

Є декілька способів детальної розбивки кривої: прямокутних координат, хорд або дотичних,продовжених хорд і т.д.

У всіх випадках детальну розбивку починають від початку і кінця до її середини.

8.2.1  Детальна розбивка кривої способом прямокутних координат

Нехай на круговій кривій радіуса R потрібно знайти точки Р₁,Р₂,Р₃ і т.д.                   

(Рис.8.4),відстані між якими по кривій рівні к.Якщо прийняти дотичну АМ за вісь абсцис,а точку А за початок вісі,то будь-яка точка на кривій буде визначатися координатами х і у.

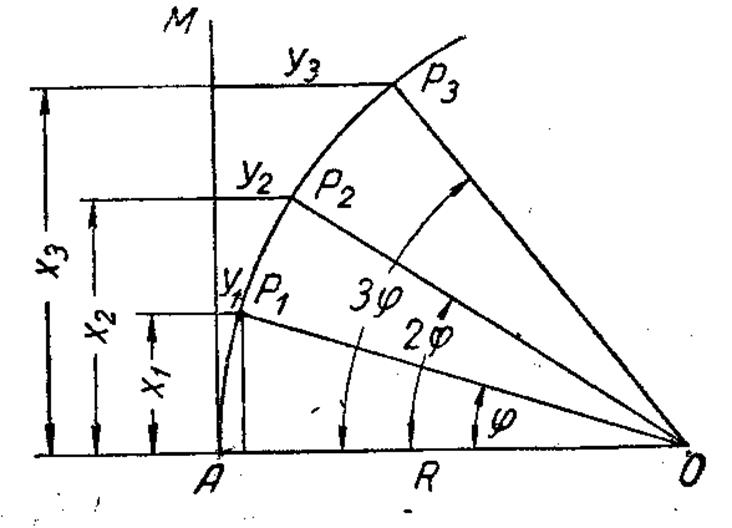
         Рисунок 8.4 - Детальна розбивка кривої способом прямокутних координат

Спочатку знайдемо значення кута φ,відповідного заданій дузі К:

                                   φ/к=360°/2πR  ,

          Звідси кут φ буде визначатися через довжину дуги так:

                                  φ =(180K)/(πR) ,                                               

             Згідно рисунку 8.  виходить,що:

х₁=Rsin φ ,   у₁ = R–R·cosφ = R(1–cos φ) = 2R·sin²φ  ,                        

х₂=Rsin2 φ,  у₂ = R−R·cos2φ = R(1–cos2φ) = 2R·sin²φ  ,

і т.д.

Побудова точок  на місцевості за допомогою теодоліту,встановленого в точці А,зводиться до відкладання по стрічці від точки А по напрямку дотичної АМ абсцис х₁ , х₂ ….,до побудови перпендикулярів до АМ за допомогою екера і відкладання на них ординат у₁ , у₂……

  Розбивку виконують від початку кривої до середини та з кінця до середини кривої.

Результати розрахунків зводяться у таблицю 8.6

Величини К-Х та У розраховуються за формулами:

X=Rsinφ                                                    (8.22)

y=R(1-cosφ);                                                 (8.23)

φ=(180K)/(πR);                                              (8.24)

де  К – інтервал розбивання 20,40,60...;

      R – радіус кривої;

      φ – кут опору на дугу відповідного інтервалам розбивки.

Інтервали детальної розбивки кривої беруться 20 м або 10 м в залежності від радіусу кривої.

При розбиванні кривої по направленню тангенсу відкладаються відрізки рівні інтервалу розбивки.