Фононы и их характеристики. Взаимодействие фононов друг на друга, взаимодействие электронов с фононами

Лекция 13

В прошлый раз мы с вами рассматривали динамику решетки, то есть что происходит с атомами, находящимися в решетке при внешнем воздействии, а в частности при тепловом воздействии. Тепловое воздействие есть всегда. Мы это рассматривали для того, что бы рассмотреть фоно-фононное и электрон-фононное рассеивание. То есть нам нужно понять, что такое фононы, какими характеристиками обладают фононы, но а дальше рассматриваем как взаимодействуют они друг с другом и как электроны взаимодействуют с фононами. Но чтобы выйти на эту терминологию – фонон, мы сначала рассматривали приближенную модель атома, модель Эйнштейна и модель одномерной фигуры. Рассматривая одномерные цепочки, мы с вами  показали зависимость частоты от волнового вектора. То есть мы с вами говорим, что если у нас есть одномерная цепочка, то по такой цепочке переносятся возбуждения, связанные с колебаниями атомов под тепловым воздействием относительно положения равновесия. Всякие процессы, связанные с колебательными распространениями в пространстве и во времени называются волновыми процессами. Мы, конечно, рассматриваем простейший случай волны – бегущая плоская волна. То есть у нас амплитуда постоянна, не зависит от координат. На прошлом занятии мы с вами получили дисперсионное уравнение. Из которого следует что частота зависит от волнового вектора. Вот если частота является функцией волнового вектора, то всякое такое уравнение называется дисперсионным. Ну и как следствие это вот частота, зависящая от скорости. Ну и если мы имеем пакет волн и дисперсию, то волны, входящие в этот пакет разбегаются, то есть каждая гармоника по-разному взаимодействует со средой.

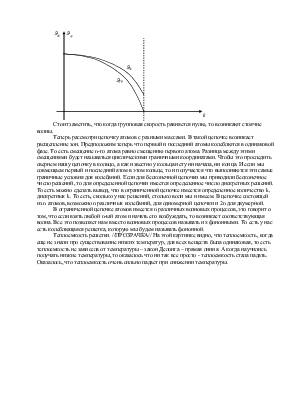
//ОПИСАНИЕ ПРОЗРАЧКИ// Верхняя картиночка говорит об этом. Дальше описываются затухательные режимы волны. Далее описываются свойства приведенной зоны Бриллюэна.

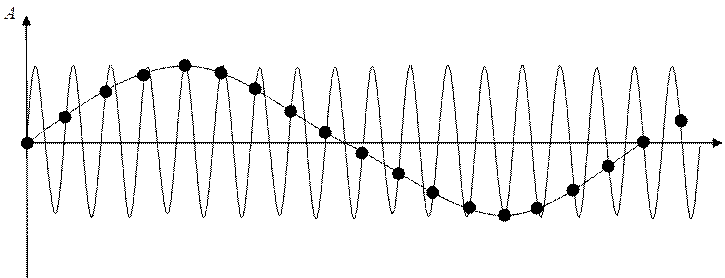
По оси абсцисс текущее направление. И вот на этом направлении есть атом, и если он находится в положении равновесия, то он будет выглядеть просто черной точкой. В перпендикулярном направлении отложено смещение. В какой-то момент времени, все атомы смещены относительно положения равновесия – совершают колебательные процессы, относительно своего положения равновесия. В какой-то момент времени можно представить, что атомы участвуют в двух волновых процессах. То есть мы имеем один колебательный, но два волновых процесса.

Поговорим теперь о фазовой и групповой скорости. Фазовая скорость – это скорость, которая характеризует распространение волнового контура, то есть все точки данного волнового контура находятся в одной волновой фазе. Групповая скорость, соответственно это скорость группы волн, которая характеризуется производной в любой точке волны. Если найти эти две скорости, то мы получим график зависимости скорости фазовой и групповой скорости от k в пределах зоны Бриллюэна.

Стоит заметить, что когда групповая скорость равняется нулю, то возникают стоячие волны.

Теперь рассмотри цепочку атомов с разными массами. В такой цепочке возникает расщепление зон. Предположим теперь что первый и последний атомы колеблются в одинаковой фазе. То есть смещение n-го атома равно смещению первого атома. Разница между этими смещениями будет называться циклическими граничными координатами. Чтобы это проследить свернем нашу цепочку в кольцо, а как известно у кольца нету ни начала, ни конца. И если мы совмещаем первый и последний атом в этом кольце, то и получается что выполняются эти самые граничные условия для колебаний. Если для бесконечной цепочки мы приводили бесконечное число решений, то для определенной цепочки имеется определенное число дискретных решений. То есть можно сделать вывод, что в ограниченной цепочке имеется определенное количество k, дискретных k. То есть, сколько у нас решений, столько волн мы и имеем. В цепочке состоящей из n атомов, возможно n различных колебаний, для одномерной цепочки и 2n для двумерной.

В ограниченной цепочке атомов имеется n различных волновых процессов, это говорит о том, что если взять любой n-ый атом и начать его возбуждать, то возникает соответствующая волна. Все это позволяет нам вместо волновых процессов называть их фононными. То есть у нас есть колеблющаяся решетка, которую мы будем называть фононной.

Теплоемкость решетки. //ПРОЗРАЧКА// На этой картинке видно, что теплоемкость, когда еще не знали про существование низких температур, для всех веществ была одинаковая, то есть теплоемкость не зависела от температуры – закон Делонга – прямая линия. А когда научились получать низкие температуры, то оказалось что ни так все просто - теплоемкость стала падать. Оказалось, что теплоемкость очень сильно падает при снижении температуры.