



Лекция 3
Связь физических свойств кристалла с его структурой
Эта связь физических свойств постулируется двумя основными принципами кристаллофизики: принцип кристаллофизики Неймана и принцип кристаллофизики Кюри. Принцип кристаллофизики Неймана говорит о том, что симметрия идеального кристалла должна обязательно содержаться в симметрии химических свойств кристалла. Этот принцип говорит о том что, если у нас есть свойство кристалла, например одно из самых важных свойств – анизотропия (разные свойства в разных направлениях). А когда мы рассматриваем структуру кристалла, мы видим что структура кристалла обладает ??? симметрией. Вот эта симметрия позволяет понять симметрично ли преобразование.
Знание симметрии кристалла, знание симметрии структуры кристалла позволяет легко описывать все дальнейшие воздействия на кристалл, процедуры воздействия на кристалл и его свойства. Поэтому описание симметрии структуры кристалла важно не только по тому что мы должны знать как выглядит структура, но и хорошо бы еще знать какая матрица симметрия у того или иного узла.
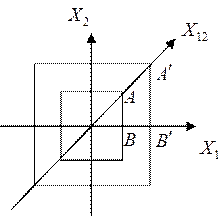 Рассмотрим как анизотропия свойств
связанна с физическими свойствами кристалла. Простой пример: рассмотрим рост
кристалла с кубической центровкой, ну в плоском варианте это у нас есть
квадрат, ну на самом деле куб, так как кубическая центровка. Вот у нас есть
элементарные кристаллик, который в определенны момент времени не попадал под
определенные параметры, под определенные размеры, а мы обсуждаем процесс его
роста. Через некоторое время он вырос, сохранив структуру кристаллической
решетки. Ясно, что исходный кристалл и вот полученный кристалл все они состоят
из каких-то примитивных, элементарных ячеек. Давайте рассмотрим два направления
Х1 и Х2. И я построй еще вот это направление, которое
обозначу Х1,2. На том самом исходном кристалле обозначим точку А, в
вершине этого квадрата и точку В. Через некоторое время точка А перемещается в
точку А’, и соответственно точка В перемещается в точку В’. Но как мы видим АА’
не равно ВВ’, но время-то одно и тоже, значит время роста по направлению Х1
и Х12 разное – скорость роста кристалла разная. По направлению Х12
скорость роста более быстрая, а по направлении Х1 более медленная.
Рассмотрим как анизотропия свойств
связанна с физическими свойствами кристалла. Простой пример: рассмотрим рост
кристалла с кубической центровкой, ну в плоском варианте это у нас есть
квадрат, ну на самом деле куб, так как кубическая центровка. Вот у нас есть
элементарные кристаллик, который в определенны момент времени не попадал под
определенные параметры, под определенные размеры, а мы обсуждаем процесс его
роста. Через некоторое время он вырос, сохранив структуру кристаллической
решетки. Ясно, что исходный кристалл и вот полученный кристалл все они состоят
из каких-то примитивных, элементарных ячеек. Давайте рассмотрим два направления
Х1 и Х2. И я построй еще вот это направление, которое
обозначу Х1,2. На том самом исходном кристалле обозначим точку А, в
вершине этого квадрата и точку В. Через некоторое время точка А перемещается в
точку А’, и соответственно точка В перемещается в точку В’. Но как мы видим АА’
не равно ВВ’, но время-то одно и тоже, значит время роста по направлению Х1
и Х12 разное – скорость роста кристалла разная. По направлению Х12
скорость роста более быстрая, а по направлении Х1 более медленная.
Для объяснения симметрии структуры и симметрии физических свойств мы будем пользоваться двумя принципами кристаллофизики.
Принцип суперпозиции Кюри: если кристалл в соответствии его физическим свойствам обладает осью симметрии и на этот кристалл подействовать каким либо внешним воздействием, то симметрия кристалла измениться, как изменяться его физические свойства. Но самое главное в принципе Кюри заключается в том, что симметрия полученного кристалла будет объединять симметрию исходного кристалла и симметрию воздействия.
Принцип симметрии Неймана – группа симметрии любого физического свойства кристалла включает элементы симметрии структуры кристалла.
Замечание: Симметрия физического свойства включает в себя структуру кристалла, а наоборот может и не быть. То есть в разных структурах кристалла могут быть не все физические свойства заданной симметрии.
Принцип симметрии Кюри: кристалл при внешнем воздействии изменяет свою точечную симметрию, но сохраняет элементы общей симметрии: симметрии структуры и симметрии воздействия.
Рассмотрим пример для осознания
принципа симметрии Кюри: у нас есть квадрат, а точнее квадратный листик, и из
него мы хотим вырезать равносторонний треугольник. На исходный листик
квадратной формы производим воздействие – вырезание равностороннего
треугольника. А теперь напишем формулы симметрии квадрата: L4L3P, теперь напишем формулу
структуры квадрата: L44P,
и формулу симметрии равностороннего треугольника: L33P.  В итоге получаем формулу: P=L44P+L33P. Что означает эта формула? Это равенство означает что мы
накладываем на симметрию квадрата симметрию равностороннего треугольника.
Значит у нас воздействие связано с вырезанием равностороннего треугольника.
Значит L33P –
симметрия воздействия, а L44P – симметрия исходного кристалла. Значит принцип Кюри
говорит что: что в результате остается кристалл, симметрия которого имеет общие
элементы симметрии с исходной структурой и симметрией воздействия. Значит
теперь можно посмотреть какие здесь будут элементы общей симметрии. Тут ось L4, а тут L3,
значит в результате у нас не будет ни L3, ни
L4. Дальше, здесь 4P,
а здесь 3P. Нужно каждую плоскость рассмотреть по
отдельности. Если какая либо плоскость является общей для исходной фигуры и для
воздействия, то она будет включена в конечную фигуру.
В итоге получаем формулу: P=L44P+L33P. Что означает эта формула? Это равенство означает что мы
накладываем на симметрию квадрата симметрию равностороннего треугольника.
Значит у нас воздействие связано с вырезанием равностороннего треугольника.
Значит L33P –
симметрия воздействия, а L44P – симметрия исходного кристалла. Значит принцип Кюри
говорит что: что в результате остается кристалл, симметрия которого имеет общие
элементы симметрии с исходной структурой и симметрией воздействия. Значит
теперь можно посмотреть какие здесь будут элементы общей симметрии. Тут ось L4, а тут L3,
значит в результате у нас не будет ни L3, ни
L4. Дальше, здесь 4P,
а здесь 3P. Нужно каждую плоскость рассмотреть по
отдельности. Если какая либо плоскость является общей для исходной фигуры и для
воздействия, то она будет включена в конечную фигуру.
Предельные группы Кюри
Предельные группы Кюри используются для описания симметрии непрерывного пространства. См. таблицу в методичке. Каждая группа является предельной для того или иного класса. У нас есть триклинная сингония – характеризуется наличием одной оси бесконечного порядка, то есть фигура вращается вокруг своей оси на 360 градусов, не совмещаясь до этого ни разу. Всего есть три фигуры вращения: конус, цилиндр и сфера, эти фигуры иллюстрируют все непрерывные среды.
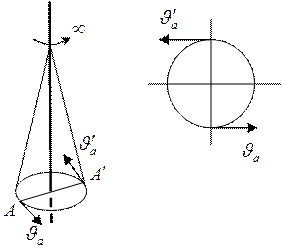 Первая предельная группа: у нас есть
ось бесконечного порядка и она по геометрическим образам соответствует конусу
вращения. Итак, если мы возьмем конус и ось, проходящая через его высоту и
будет осью вращения бесконечного порядка, и будем вращать конус вокруг оси. Так
образом мы убирает плоскость симметрии зеркального отражения. Во вращающемся
конусе относительно данной оси нет плоскостей симметрии. Вторая предельная
группа: L умножить на
бесконечность - L∞. И вот эта запись говорит
о том, что здесь есть ось бесконечного порядка, а второе что параллельно данной
оси есть бесконечное число плоскостей зеркального отражения.
Первая предельная группа: у нас есть
ось бесконечного порядка и она по геометрическим образам соответствует конусу
вращения. Итак, если мы возьмем конус и ось, проходящая через его высоту и
будет осью вращения бесконечного порядка, и будем вращать конус вокруг оси. Так
образом мы убирает плоскость симметрии зеркального отражения. Во вращающемся
конусе относительно данной оси нет плоскостей симметрии. Вторая предельная
группа: L умножить на
бесконечность - L∞. И вот эта запись говорит
о том, что здесь есть ось бесконечного порядка, а второе что параллельно данной
оси есть бесконечное число плоскостей зеркального отражения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.