Непрерывность, дифференцируемость и интегрирование случайных процессов

Глава 6. Непрерывность, дифференцируемость и интегрирование случайных процессов

Для детерминированных функций важнейшими свойствами являются непрерывность, дифференцируемость, существование интеграла. Рассмотрим, как они определяются для случайных процессов.  Перечисленные свойства связаны с операцией предельного перехода и понятием предела последовательности СВ, которое в отличие от обычного понятия сходимости последовательности, рассматриваемого в математическом анализе, зависит от принятого критерия сходимости. Поясним сказанное более подробно.

Говорят, что последовательность СВ x₁, x₂, …, x_п сходится по вероятности к СВ x, если для любого e > 0  или . Если последовательность сходится по вероятности к СВ x, то последовательность ПВ W_xn(x) сходится при п ®¥  в обычном смысле к W_x(x). Если x = а – детерминированная величина, то последовательность {W_xn(x)} сходится к d(х – а). Сходимость по вероятности обозначают как  (по вер.) или .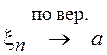

Другой вид сходимости последовательности СВ – это сходимость в среднеквадратическом, определяемая как 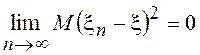 или , где обозначение l. i. m. – аббревиатура английского названия этого предела (limit in the mean square). Если x = а, то учитывая, что

 =

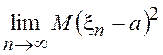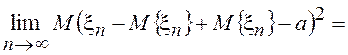
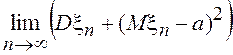
и тот факт, что предел суммы двух неотрицательных слагаемых равен нулю только, если предел каждого слагаемого равен нулю, получим

, .

Таким образом, предел средних значений СВ x_п есть а, а предел их дисперсий равен нулю.

Для последовательности ПВ W_xn(x) полученное условие означает сходимость W_xn(x) к d(х – а), т. е. сходимость по вероятности. Обратное утверждение в общем случае неверно, так как среднеквадратическая сходимость предполагает конечность , а это требование не всегда выполняется.

Теперь мы подготовлены к тому, чтобы дать определение непрерывности и дифференцируемости случайного процесса.

Случайный процесс x(t) называется непрерывным в точке t в среднеквадратическом, если 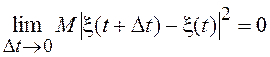. Если это условие выполняется для всех t Î [a, b], то процесс x(t) называют непрерывным на этом интервале. Необходимым и достаточным условием непрерывности процесса в точке t  является непрерывность его корреляционной функции K_x(t₁, t₂) при
t₁ =  t₂ = t. Для стационарного процесса это означает непрерывность корреляционной функции K_x(t) в нуле.

Случайный процесс дифференцируем в точке t в среднеквадратическом и имеет производную x¢(t), если

.

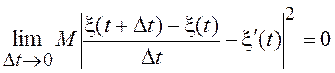Учитывая связь между сходимостью в среднеквадратическом и по вероятности, можно утверждать, что СП, непрерывный и дифференцируемый в среднеквадратическом, будет непрерывным и дифференцируемым и по вероятности.

Необходимым и достаточным условием дифференцируемости случайного процесса будет существование и непрерывность второй смешанной производной корреляционной функции СП 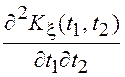, которая определяет корреляционную функцию процесса x¢(t), т. е.

.

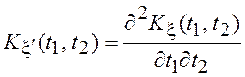Для стационарного процесса

.

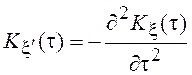За счет чего появился знак минус, предлагаем догадаться читателю. Учитывая, что , где , а F – оператор Фурье, получим, что спектральная плотность производной

.

Из рассмотренных выше примеров случайных процессов “белый” шум является разрывным, недифференцируемым процессом (рис. 25, а); процесс с “Лоренцевским” энергетическим спектром (рис. 25, е) является непрерывным, но недифференцируемым. Остальные рассмотренные процессы непрерывны и дифференцируемы.

Рассмотрим вопрос о взаимной корреляционной функции процесса x(t) и его производной x¢(t). Считая процесс дифференцируемым в среднеквадратическом, можно показать, что

.

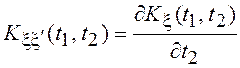Для стационарного процесса

.

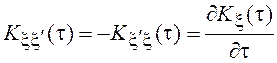Преобразование Фурье взаимной КФ даст взаимный энергетический спектр процесса и его производной, который в силу свойств преобразования Фурье будет равен

.

Так как корреляционная функция стационарного СП является четной, то  – нечетная функция, т. е. = – и = 0. Таким образом, значения дифференцируемого СП в совпадающие моменты времени (t₁ =  t₂ = t, t = 0) некоррелированы.

Рассмотрим вопрос об интегрировании случайных процессов.

Изучим сначала линейный функционал от СП x(t) вида 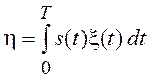, где s(t) – детерминированная функция. Записанный интеграл есть случайная величина, к которой при  в среднеквадратическом сходится последовательность СВ

, .

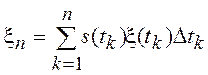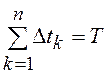Среднее значение и дисперсия этой случайной величины равны соответственно

, .

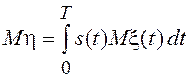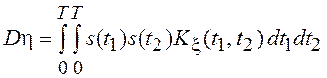Для стационарного случайного процесса

М{x(t)} = const; , и следовательно,

;   .

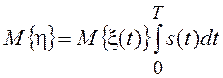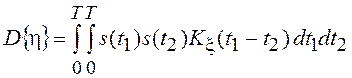Если Мx(t) = 0, то .

При t_k << T в силу центральной предельной теоремы распределение W_h(x) будет близко к нормальному с параметрами   и . Для “белого” шума, у которого Мx(t) = 0, а 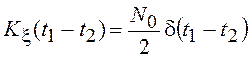, нормальная СВ h будет иметь  = 0 и  = .

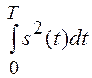Часто приходится рассматривать неопределенный интеграл от стационарного случайного процесса 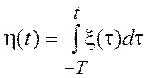. Записанное выражение можно рассматривать как результат действия оператора Вольтерра с ядром, тождественно равным единице. Более общим случаем будет реакция линейной системы с импульсной характеристикой  на стационарный случайный процесс x(t), т. е. 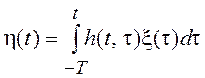. Среднее значение и корреляционная функция данного СП будут равны соответственно

,

.

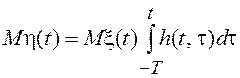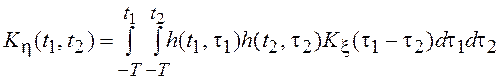Как видно из приведенных выражений, процесс  нестационарный, так как среднее значение зависит от времени.

Если линейная система стационарна (имеет постоянные параметры), то = и в установившемся режиме (Т = ¥) процесс  будет стационарным в широком смысле. Его математическое ожидание

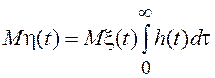
не зависит от времени, а корреляционная функция  будет зависеть от разности . Убедиться в этом мы предлагаем читателю. Для “белого” шума , а КФ определяется выражением

=

.

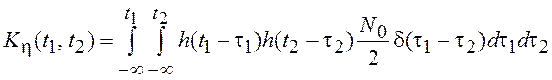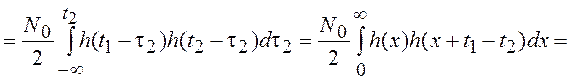
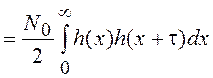Дисперсия процесса  будет равна в этом случае

(t) = =.

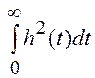Для процесса 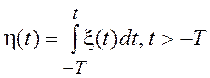 среднее значение и дисперсия будут равны соответственно

;

.

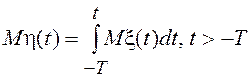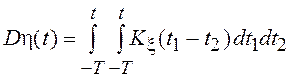Для “белого” шума , а дисперсия (t) =.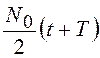

В установившемся режиме для стационарной линейной системы при отыскании корреляционной функции на выходе можно воспользоваться частотным методом, заменив в выражении

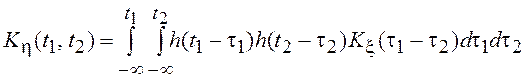
корреляционную функцию  ее представлением через спектральную плотность :

=.

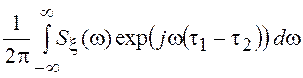Таким образом,

.

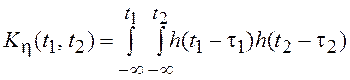
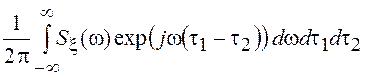Меняя порядок интегрирования по ₁, ₂ и w и учитывая, что

; ,

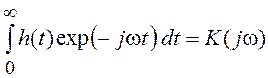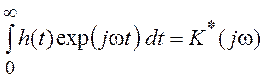где K(jw) – коэффициент передачи линейной системы, получим окончательно:

,

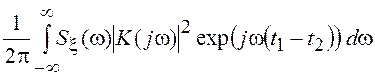откуда видно, что  действительно зависит от разности , а произведение   является спектральной плотностью процесса :

= .

Контрольные вопросы

1. Какие виды сходимости последовательностей СВ Вам известны?

2. Дайте определение непрерывности СП в точке и в области.

3. Сформулируйте необходимые и достаточные условия дифференцируемости СП.

4. Какой вид имеют взаимная корреляционная функция и взаимный энергетический спектр процесса и его производной?

5. Как связаны между собой корреляционная функция стационарного СП и его производной? Какова связь между энергетическими спектрами СП  и ?