Лекция 7
Идеология приведения к одночастичной задачи называется метод Хартрифока.
Берем одномерный кристалл, или одно направление в кристалле. В этом случае мы знаем что: задача изотропна, задача сферически симметрична, т.е. не зависит от направления.
 Между частицами действует закон Кулона.
Нарисовав такую картину ищем что происходит в результате взаимодействия,
электронов принадлежащих двум соседним атомам.
Между частицами действует закон Кулона.
Нарисовав такую картину ищем что происходит в результате взаимодействия,
электронов принадлежащих двум соседним атомам.
Волновая функция Блоха является решением уравнения Шредингера для периодически повторяющихся потенциальных барьеров прямоугольной формы. Найдем еще значение для свободной частицы:
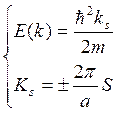
Энергий свободной частицы мы
видим что это парабола, кривизна парабола маленькая, а радиус кривизны большой.
Откладываем на положительном и отрицательном направлениях вектор трансляции
равный ![]() , и от них проводим вертикальные линии
вверх. Существует понятие мощность потенциального барьера она равна
произведению
, и от них проводим вертикальные линии
вверх. Существует понятие мощность потенциального барьера она равна
произведению ![]() на ширину барьера А. Есть два частных
случая, когда мощность потенциального барьера стремиться к нулю, это свободная
частица и мощность потенциального барьера стремиться в бесконечность это
связанная частица. Если
на ширину барьера А. Есть два частных
случая, когда мощность потенциального барьера стремиться к нулю, это свободная
частица и мощность потенциального барьера стремиться в бесконечность это
связанная частица. Если ![]() то за счет туннельного
эффекта происходит передача этой волновой функции. По мере приближения к
волновому вектору
то за счет туннельного
эффекта происходит передача этой волновой функции. По мере приближения к
волновому вектору ![]() , происходит явление Брэковское
отражение волн от атомов плоскостей.
, происходит явление Брэковское
отражение волн от атомов плоскостей.
Электронная волна – волна вероятности. Электрон это квант электронной волны, это квази частица. Электронные волны взаимодействуют с ионами в узлах решетки и отражаются. Падающие и отраженные электронные волны образуют стоячие волны. Ее скорость состоит из фазовой и групповой. Фазовая скорость это скорость точек в одной фазе. Когда говорят о группе волн то говорят о групповой скорости.
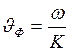 -фазовая
скорость
-фазовая
скорость
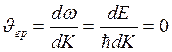 -групповая
скорость
-групповая
скорость
где К – волновое число и равно ![]() , а
, а ![]() -
частота колебаний
-
частота колебаний
для стоячей волны групповая скорость должна быть равна нулю, а следовательно производная имеет экстремум.
Решение уравнения Шредингера рассматривается на метод слабой связи и метод сильной связи.
Вывод:
1. Зависимость Е(к) имеет
разрывы функции. Разрывы функции при 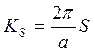 .В зависимости Е(к)
делится на зоны разрешенных состояний и зоны неразрешенных. Е(к) представляет
энергетический спектр, с чередованием разрешенных и запрещенных зон
чередования. Запрещенные зоны иначе называются щели. Физический смысл щелей в
энергетическом спектре говорит о том, что электронные волны, с соответствующими
волновыми значениями, могут распространяться по кристаллу, они затухают. Зоны разрешенных
состояний как раз такие электронные волны, с такими волновыми векторами могут
иметь место.
.В зависимости Е(к)
делится на зоны разрешенных состояний и зоны неразрешенных. Е(к) представляет
энергетический спектр, с чередованием разрешенных и запрещенных зон
чередования. Запрещенные зоны иначе называются щели. Физический смысл щелей в
энергетическом спектре говорит о том, что электронные волны, с соответствующими
волновыми значениями, могут распространяться по кристаллу, они затухают. Зоны разрешенных
состояний как раз такие электронные волны, с такими волновыми векторами могут
иметь место.
Зона Бриллюэна
Это зона периодических значений
волнового вектора К. При S=1 мы будем иметь первую зону
Бриллюэна 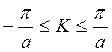 , вторая зона это область от
, вторая зона это область от ![]() на положительном направлении, и вторая
зона включает первую, следовательно размер второй зоны такой же как первый. Все
зоны Бриллюэна имеют одинаковые размеры
на положительном направлении, и вторая
зона включает первую, следовательно размер второй зоны такой же как первый. Все
зоны Бриллюэна имеют одинаковые размеры ![]() .
Каждому состоянию Бриллюэна соответствует разрешенному состоянию для
электронных волн.
.
Каждому состоянию Бриллюэна соответствует разрешенному состоянию для
электронных волн.
Обратное пространство. Пространство волнового вектора
Электронная волна ![]() . Любая частица создается своей обобщенной
координатой q, и импульсом р. Координаты q представляют собой прямое, координатное пространство, а то,
в котором откладывается импульс, называется импульсным пространством, и по
размерности оно представляет собой обратное пространство. В прямом пространстве
мы имеем три базисных вектора a,b,c, так же знаем углы между ними
. Любая частица создается своей обобщенной
координатой q, и импульсом р. Координаты q представляют собой прямое, координатное пространство, а то,
в котором откладывается импульс, называется импульсным пространством, и по
размерности оно представляет собой обратное пространство. В прямом пространстве
мы имеем три базисных вектора a,b,c, так же знаем углы между ними ![]() , и
таким образом задаем прямую решетку. Элементарная ячейка обратного
пространства, будет строиться на базисных векторах обратного пространства. Переход
от прямого к обратному пространству:
, и
таким образом задаем прямую решетку. Элементарная ячейка обратного
пространства, будет строиться на базисных векторах обратного пространства. Переход
от прямого к обратному пространству:
![]() введем вектор трансляции в
обратном пространстве
введем вектор трансляции в
обратном пространстве ![]()
где
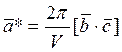
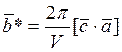
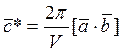 .
.
Элементарная ячейка обратного пространства
Базисные векторы а и b. Выбираем узел 0. Выберем ближайшие к этому узлу, пересечения лежащие вокруг. Теперь соединяем узел 0 отрезком с узлом 1, после этого этот отрезок делим пополам и проводим через середину прямую перпендикулярному этому отрезку. Эту процедуру повторяем для всех ближайших выбранных к этому узлу узлов. И получаем площадь, ограниченную шестиугольником.

Приведенная зона Бриллюэна
Периодически повторяющееся обратное пространство. В этом пространстве есть элементарные ячейки – это и есть зоны Бриллюэна. Но раз все повторяется, значит, все, что выходит за пределы первой зоны, во вторую и в третью, можно привести в первую зону.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.