Поверхность Ферми. Кинетические свойства твердых тел

Лекция 10

Поверхность Ферми

Итак, мы знаем, что электронный газ в металлах (твердых телах), которыми мы занимаемся, описывается, как привило квантовой статистикой Ферми-Дирака. При высоких температурах, когда может сняться вырождение, мы будем описывать его статистикой Максвелла-Больцмана. Но, однако, для полупроводников работает статистика Максвелла-Больцмана, а вот для металлов, как правило, никогда вырождение не снимается. Для описания статистических свойств электронного газа работает статистика Ферми-Дирака и функция распределения по состояниям E_n, или можно говорить о среднем числе частиц в данном состоянии. Для среднего числа значение может быть любое, а для реального только целое.

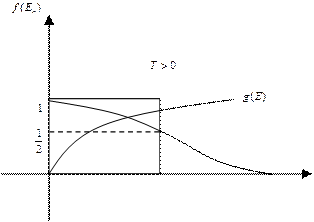
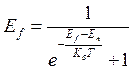
Теперь мы переходим в К пространство. Мы знаем что есть, по сути, электронные волны, поэтому все поведение электронов в смысле волновых свойств определяется его координатой волнового вектора k_x, k_y, k_z. Любая точка в этом пространстве, заданная такими координатами есть ни что иное, как электронная волна. Если рассматривать изотропный случай, то можно построить в пространстве волнового вектора несколько изоэнергетических поверхностей. Изоэнергетическая поверхность – поверхность в каждой точке, которой энергия будет являться функцией константы. Не трудно видеть, что если мы рассматриваем изотропный случай, то эта поверхность будет иметь смысл сферы.

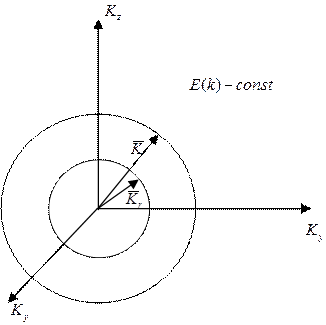
Вот здесь какому-то значению к соответствует энергия, они связаны :(h²k²)/2m. Так вот это векторы энергетической поверхности. Выделим в этом пространстве такую энергетическую поверхность, для которой значение энергии равно энергии ферми. Так вот это получилось поверхность, в которой энергия соответствует энергии Ферми и называется поверхностью ферми.

Поверхностью ферми называется изоэнергетическая поверхность в к пространстве, для которой энергия равна энергии ферми. Рассмотрим теперь температуру абсолютного нуля. При такой температуре все значения энергии En меньше энергии ферми заняты F(E)=1, а все значения энергии больше энергии ферми свободны, то есть F(E)=min. Уровень ферми определяется исходным количеством электронов. Кроме поверхности ферми в к пространстве есть и элементарная ячейка к пространства, обратного пространства, это есть зона Бриллюэна. И вот здесь возникает очень интересное явление: есть две области в к пространстве. Одна область ограничена значением энергии равной значению энергии ферми, а вторая информация связанна с элементарной ячейкой обратного пространства. K ферми (зависит от числа электронов) и k Бриллюэна (зависит от размеров решетки). Поверхность ферми ограничивает область в k пространстве занятую электронными состояниями. При температуре абсолютного нуля электрон движется только по поверхности ферми. На самом деле он двигается в k пространстве, так что его модуль волнового вектора не меняется, он все время равен фермиевскому значению, а направление его меняется.

Скорость вектора. Данную формулу можно определить через классические вещи, понимая, что импульс равный hk ферми равен mVферми. Эта два импульса квазичастиц.

Несколько слов о теплоемкости электронного газа. Опять же что бы определить теплоемкость электронного газа, нужно вспомнить, что валентность есть тетродинамический ?? потенциал, который определяет скорость изменения внутренней энергии  при изменении температуры.

Кинетические свойства твердых тел

Кинетические свойства твердых тел - кинетика, движение. Все что мы рассматривали до этого, все в статистическом смысле, говорилось о состоянии равновесия. Электрон теперь будем описывать как квантовую частицу – частицу, которая обладает квантовыми свойствами. Мы знаем, что нельзя сказать достоверно, где находится электрон, в какой точке. Для его описания нам необходимо знать волновую функцию ς(k) и соответствующую энергию E(k). А вот теперь на такую систему наложим внешнее воздействие: электрическое и тепловое поле. Всякое движение любой частицы связанно с наличием силы. Есть сила, есть движение. Всякое силовое воздействие возможно, если есть градиент. Всякая сила есть градиент потенциала. Если у нас есть некое потенциальное воздействие и есть градиент, то есть сила. Электрическое поле это градиент электрического потенциала – gradφ, а тепловое поле – gradT. И третий случай градиента может быть следующий: когда есть градиент концентрации, то есть в одном месте много частиц, а в другом мало – диффузия. Итак, у нас будут диффузионные потоки, тепловые потоки и потоки электрического заряда. Потоки электрического заряда принято называть электрическим током, потоки теплового заряда так, и будут тепловыми потоками, а градиент концентрации в нашем случае будет очень сильно влиять на градиент электрического поля. Потому что градиент концентрации – в одном месте электронов много – электрический заряд большой, в другом месте мало – электрический заряд маленький. Значит, получается, что в одном месте один потенциал, а в другом другой потенциал. То есть градиент концентрации обязательно будет создавать, то есть это градиент концентрации заряженных частиц, ни каких- ни будь других – нейтральные частицы не будут создавать градиент электрического поля, а вот если мы рассматриваем градиент концентрации заряженных частиц электронов, то обязательно возникнет градиент электрического потенциала. Существуют уравнения Ансадиана (???) говорят о том, что любой поток связан с градиентом поля. В нашем случае есть твердое тело, у которого есть электрические заряды, решетка, и мы накладываем какое ни, будь электрическое поле, или будем нагревать в каком либо месте, то есть у нас будет два градиента и gradφ и, gradT. Отсюда следует, что поток, на самом деле рассматривают не просто поток, а удельный поток – единица объема на единицу площади, так вот удельный поток электрического заряда параллельный поперечному сечению – есть плотность электрического тока. Она будет пропорциональна gradφ и gradT. Они будут связаны кинетическими коэффициентами пропорциональности: L_EE и L_ET. Поток электрического заряда, то есть электрический ток, плотность электрического тока будет пропорциональна gradφ и L_EE, gradT и коэффициенту L_ET. И соответственно удельный тепловой поток, то есть это единица тепла, на единицу времени через данное поперечное сечение. Первое уравнение обуславливает поток электрического заряда за счет электрического поля, а второе  поток электрического заряда за счет градиента температуры. Уравнение дает поток тепла за счет присутствия градиента электрического поля, а другое уравнение – поток тепла за счет теплового потока. В это выражаются два известных закона – закон Ома и закон Фурье. Значит можно сделать вывод, что L_EE есть ни что иное, как теплопроводность. Если L_EE и L_ET стремятся быть соизмеримы, то говорят о термо-электро-градиентных явлениях.