Метод сильной связи. Классификация твердых тел по проводимости

Лекция 8

В прошлый раз мы рассматривали метод слабой связи, которая использует модель Коникера-Пелли, хотя на самом деле эта модель включает и метод сильной связи вот для тех самых внутренних электронов когда мощность потенциального барьера стремиться к бесконечности. Зона Бриллюэна возникает всегда, когда мы рассматриваем периодические структуры. Ну например для электрона это особое облако в котором происходит та самая электронная дифракция, и мы видим результат взаимодействия дифракционных волн с атомами окружающей среды. В рамках примененной зоны Бриллюэна мы можем проследить, что вся информация о зонном строении энергетического спектра присутствует. В начале темы говорилось, что энергетический спектр электронов в кристалле - основы зонной теории. Так вот зонная теория и есть тот самый вывод из решения уравнения Шредингера для кристаллов. Основная информация это волновая функция и собственное её значение – то есть кинетическая энергия. Мы будем рисовать значение энергетического спектра E(k) в пределах приведенной зоны Бриллюэна, для одномерного кристалла. Границы зоны Бриллюэна: , и вот эта картинка будет нас всегда в дальнейшем преследовать, так как она будет всегда изначальной во всех наших рассуждениях.

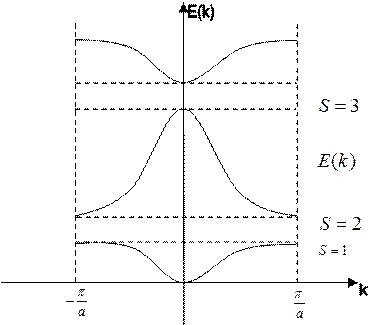
Главный вывод из модели слабой связи – это информация явный вид зависимость E(k) в пределах приведенной зоны Бриллюэна. Это нам потребуется, потому что мы увидим, как вот этот реальный результат определяет эффективную массу электрона. Главное знать, что спектр E(k) является дискретным, то есть не непрерывным, есть зона разрешенных значений и зона запрещенных значений. В пределах естественно разрешенной зоны есть некая зависимость E(k). Как правило, эти гармонические кривые являются либо синусом, либо косинусом.

Метод сильной связи

Поговорим теперь о методе сильной связи. Исходной является зависимость потенциального рельефа U(r) для одномерного кристалла, это исходная информация, поэтому от нее никуда не деться, но сейчас мы добавим следующие рассуждения: добавляем на рисунок значения энергии, которые говорят о дискретном нахождении электронов в вакууме, это информация для дискретных энергетических уровнях в вакууме. Принцип Паули утверждает что на одном энергетическом уровне может находиться два электрона, где n-главное квантовое число. Метод сильной связи принципиален для тех электронов, которые находятся на нижних энергетических уровнях, то есть у них энергия электрона много меньше высоты потенциального барьера, и над барьером такие электроны двигаться не могут и они могут участвовать только в туннельном процессе, то есть туннельный эффект, обеспечивающий 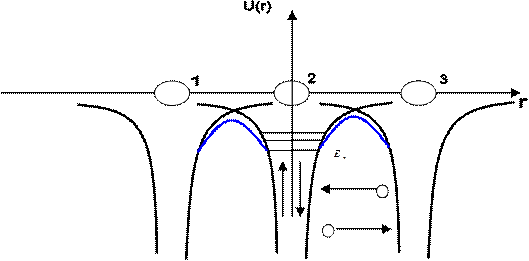обмен между электронами принадлежащим разным ядрам – главная идея для вот этих самых электронов. За счет обменного взаимодействия электронами двух соседних атомов происходит не просто изменение потенциального элемента, но еще происходит и расщепление соседних энергетических уровней. В простейшем случае, когда решается задача для двух соседних атомов говориться о том, что обменное взаимодействие обеспечивает расщепление каждого уровня на два подуровня, так чтобы атомы обменялись электронами.

Теперь рассмотрим еще одну прозрачку, где у меня представлены энергетические уровни отдельно взятого атома. Как выглядит энергетический спектр от расстояния между атомами. Если расстояние стремится в бесконечность, имеет смысл говорить об одиночно взятом атоме. И для одиночно взятого атома мы знаем вот этот самый потенциальный рельеф, то есть мы знаем информацию об энергетических уровнях E_n для одиночного атома, ну и пускай это будут какие-то уровни E₁, E₂, E₃, Е₄. Вот это и есть информация об одиночно взятом атоме. За счет объемного взаимодействия мы говорим что изменяется высота потенциального барьера, и отдельно взятые уровни понижаются. А затем происходит расщепление. Если у нас два атома взаимодействуют, то каждый уровень расщепляется на два подуровня. При том расстояние оно увеличивается. Если у нас взаимодействуют одновременно три электрона, то соответственно будет три подуровня. Соответственно если взаимодействуют n электронов, то расщепляется на n подуровней. Значит, мы видим, что за счет этого обменного взаимодействия туннельного эффекта все энергетические уровни отдельно взятых электронов расщепляются на зоны разрешенных состояний. Расстояния между разрешенными зонами представляют собой запрещенные зоны. И возникает такое явление, когда две соседние зоны могут перекрыться. Если зоны не пересекаются, то на каждом из n уровней может находиться пара электронов с разным спином. Поэтому у всего электрона электронное состояние в каждой разрешенной зоне 2n, где n-число атомов.

Дискретный спектр -  спектр разрешенных и запрещенных состояний.

Классификация твердых тел по проводимости

Все материалы делятся на две большие группы: проводники и непроводники. Что бы материал был проводником нужны свободные электроны (свободны они только тогда, когда есть разрешенные состояния). Если в зоне разрешенных состояний во первых есть электрон и часть разрешенных состояний свободна от электронов, то тогда можно говорить о том что будет проводимость. Если в зоне разрешенных состояний нет свободных состояний даже при наличии электронов, электроны не могут менять сове состояние, тогда мы будем говорить о непроводнике. Теорема Макентора: если мы имеем четную валентность материала, то тогда этот материал будет непроводник, а если нечетная валентность, то тогда будет проводником. Разрешенная зона, частично заполненная  называется зоной проводимости.

Эффективная масса

Когда мы с вами рассматриваем одномерное уравнение Шредингера в полярных координатах. Получаем в результате его решения для заданных U(R), получаем зависимости E(k). Метод эффективной массы заключается в том, что когда мы рассматриваем свободное пространство, то есть потенциальный рельеф отсутствует, U(R)=0. Приближение эффективной массы полагает это.