Коаксиальная линия. Волны в направляющих структурах при произвольной нагрузке

Оглавление

1. КОАКСИАЛЬНАЯ ЛИНИЯ.......................................................... 2

1.1. Поле Т-волны в коаксиальной линии..................................... 2

1.2. Погонные параметры коаксиальной линии........................... 3

2. ВОЛНЫ В НАПРАВЛЯЮЩИХ СТРУКТУРАХ ПРИ ПРОИЗВОЛЬНОЙ НАГРУЗКЕ.................................................................. 6

2.1. Коэффициент отражения и импеданс..................................... 6

2.2. Суперпозиция падающей и отраженной волн....................... 7

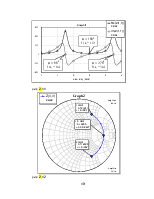
2.3. Круговая диаграмма............................................................... 10

2.4. Порядок выполнения работы................................................. 14

2.5. Контрольные вопросы............................................................. 19

 1. КОАКСИАЛЬНАЯ ЛИНИЯ

1.1. Поле Т-волны в коаксиальной линии

Главное свойство поля Т-волны – отсутствие продольных компонент электрического и магнитного полей. Т-волна может существовать только в линиях, образованных как минимум двумя однородными в продольном направлении проводниками. Электрическое поле Т-волны в поперечном сечении совпадает с решением электростатической задачи, потенциально (может быть представлено градиентом скаляра – потенциала), что дает возможность определить напряжение (разность потенциалов) между проводниками как работу сил поля при перемещении пробного заряда по произвольному, но лежащему в плоскости поперечного сечения контуру между проводниками. Магнитное поле Т‑волны в поперечном сечении линии совпадает с решением стационарной задачи для тока, протекающего по проводникам. Поэтому и в динамическом поле бегущей волны допустимо определение тока как циркуляции вектора напряженности магнитного поля по произвольному, но лежащему в плоскости поперечного сечения и охватывающему один из проводников контуру.

Т-волны не имеют дисперсии, скорость их всегда равна скорости света в среде, заполняющей линию.

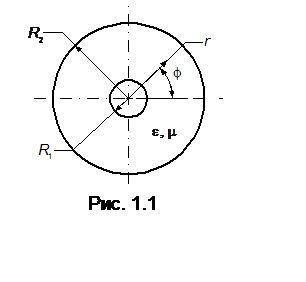
Коаксиальная линия представляет один из наиболее распространенных типов линии с Т-волной. Коаксиальная линия образована двумя соосными цилиндрическими проводниками (рис. 1.1). В такой линии могут распространяться как основная Т-волна, так и волны высших типов. Если же l > p(R₁ + R₂), то высшие типы не распространяются и в линии представлена лишь основная Т-волна (одномодовый режим).

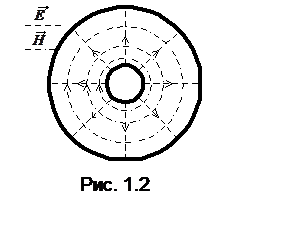Поперечная структура поля Т-волны (рис. 1.2) довольно проста и обладает осевой симметрией. Как и положено поперечной волне, ее электрическое и магнитное поля не имеют продольных компонент. Силовые линии электрического поля направлены по радиусам, силовые линии магнитного поля образуют концентрические окружности. Поле отлично от нуля только во внутреннем пространстве между проводниками (R₁ < r< R₂).

Часто вводят понятие электрической длины отрезка линии Q = kDz.

1.2. Погонные параметры коаксиальной линии

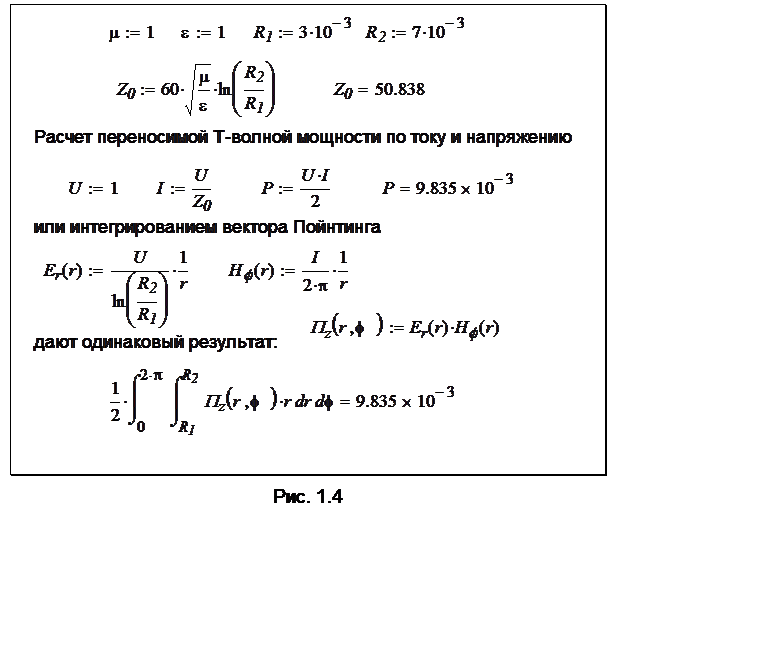Поле Т-волны в коаксиальной линии – динамическое, однако в плоскости поперечного сечения распределение электрического поля совпадает с распределением электростатического поля цилиндрического конденсатора, а магнитного поля – с полем постоянного тока в коаксиальных проводниках. Как уже отмечалось, в таких условиях можно определить напряжение и ток в линии. Также можно, используя формулы (1.1), найти энергию, запасенную в электрическом и магнитном полях короткого отрезка линии, и связать их соответственно с напряжением и током. Рис. 1.5 иллюстрирует лишь расчет погонной емкости, аналогичный материал по расчету погонной индуктивности

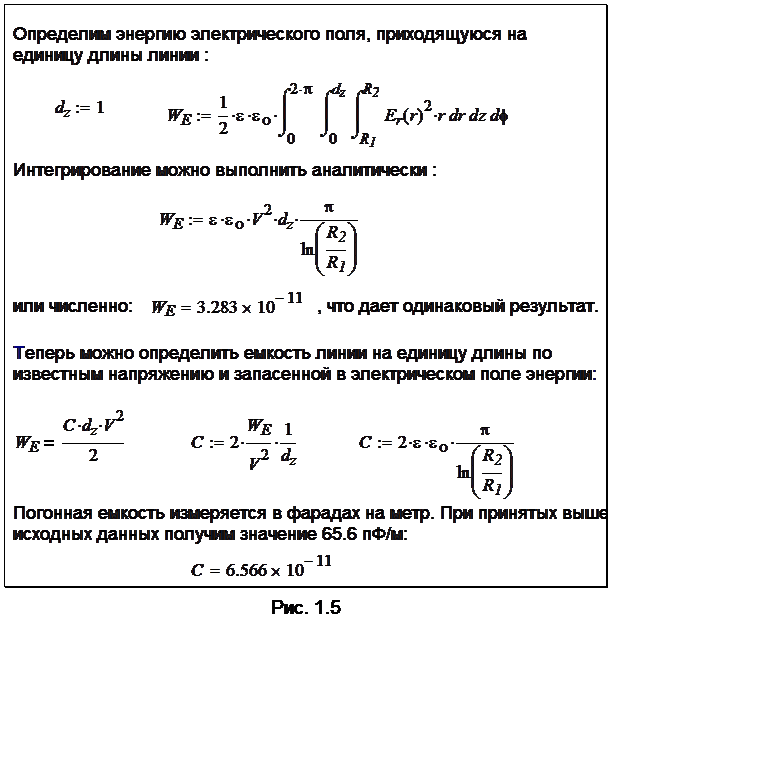
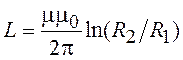                                                                                (1.2)
представлен в [   ].

Волновое сопротивление Z₀ и фазовую скорость v в линии с
Т-волной можно определить через погонные параметры:

,                           .                         (1.3)

Учитывая формулу (1.2) и выражение для погонной емкости на рис. 1.5, для коаксиальной линии получим:

.

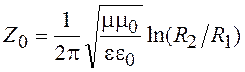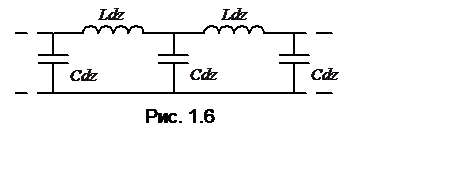Определение погонных параметров позволяет ввести в рассмотрение условную эквивалентную схему линии с Т-волной (рис. 1.6).

2. ВОЛНЫ В НАПРАВЛЯЮЩИХ СТРУКТУРАХ ПРИ ПРОИЗВОЛЬНОЙ НАГРУЗКЕ

2.1. Коэффициент отражения и импеданс

Общее решение классического волнового уравнения

                            
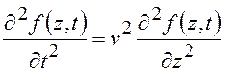
представляет собой совокупность одинаковых, но бегущих в противоположных направлениях волн:, где v – скорость волн, F – функция, описывающая профиль волны.

Для монохроматических волн можно не рассматривать зависимость от времени (она гармоническая) и использовать комплексные амплитуды. В бегущей волне, если нет потерь, модули амплитуд напряжения и тока определяются мощностью и не зависят от продольной координаты. Фаза же линейно зависит от продольной координаты.