Методические указания к выполнению лабораторной работы «Согласование нагрузки»

Методические указания к выполнению лабораторной работы «Согласование нагрузки»

1. Теоретические сведения

            В радиотехнических устройствах часто цепь, потребляющая высокочастотную (ВЧ) энергию (нагрузка) находится на удалении от источника этой энергии. В этом случае энергия передается с помощью линии передачи (ЛП). Выбор волновых сопротивлений ЛП ограничен несколькими стандартными номиналами ( для коаксиального кабеля это 50. 75, 90, 150 Ом), в то время как сопротивление (проводимость) нагрузки может быть самым разным. Очевидно, что для обеспечения эффективной передачи энергии в нагрузку необходимо иметь в ЛП режим бегущей волны, а для этого ее входное сопротивление (проводимость) должно равняться волновому сопротивлению (проводимости). Задача трансформации сопротивления (проводимости) для удовлетворения этого условия реализуется с помощью согласующего устройства. Подобная же проблема должна решаться в случае, если выходное сопротивление (проводимость) предыдущей цепи не равно входному сопротивлению последующей цепи. Согласующие устройства могут выполняться в виде цепей из сосредоточенных реактивностей (обычно на не очень высоких частотах) или из отрезков ЛП. Последний вариант обычно реализуется на СВЧ.

            В данной работе исследуется простейший способ согласования с помощью двух отрезков ЛП, называемый «одношлейфным согласованием.  Идея его чрезвычайно проста.

            Известно, что проводимость  на входе отрезка ЛП без потерь длиною  на частоте , нагруженной на нагрузку с проводимостью , может быть определена как:

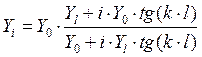,где - волновая проводимость ЛП, 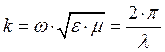 . Так как функция  меняется от  до  то, в зависимости от длины отрезка ЛП, значение  будет комплексным  (предполагается, что  содержит вещественную часть) и его вещественная и мнимая части могут принимать самые разные значения. Выберем такую длину отрезка ЛП, чтобы вещественная часть  была бы равна . Тогда  получим следующие уравнения для  и :   ,    .

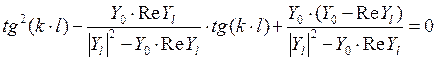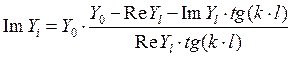Таким образом, на входе этого отрезка ЛП вещественная часть проводимости равна . Для того, чтобы обратить мнимую составляющую этой проводимости в ноль, достаточно в этой точке присоединить проводимость равную   . Следовательно, теперь в ЛП до согласующего устройства будет существовать бегущая волна. Обычно для нахождения длины  отрезка ЛП и входной реактивности  пользуются не приведенными выше уравнениями, а так называемой диаграммой Вольперта-Смита (ДВС). В 1938 г., независимо друг от друга, американский инженер Смит и советский ученый Вольперт опубликовали статьи, описывающие эту диаграмму.  По существу, ДВС есть графическое представление уравнения для .  Вид ДВС представлен на рис. 1. Окружности разного диаметра, соприкасающиеся в одной точке внизу, представляют собой линии равного активного сопротивления (проводимости). Линии, расходящиеся веером вправо и влево, представляют собой линии равного реактивного сопротивления (проводимости). В правой половине ДВС откладываются положительные реактивности, в левой – отрицательные. На внешней окружности откладываются расстояния вдоль ЛП в долях длины волны или в градусах. Перемещение вдоль ЛП на половину длины волны соответствует перемещению по полному периметру этой окружности. На «бумажных» ДВС откладываются нормированные  значения сопротивлений (нормированные  значения проводимостей). На ДВС в компьютерных программах часто значения на кривых являются абсолютными. Центр диаграммы соответствует чисто активному сопротивлению (проводимости) равному волновому. ДВС для сопротивлений и проводимостей практически полностью совпадают. Нужно только учитывать, что положительное реактивное сопротивление соответствует  индуктивности, а положительная реактивная проводимость соответствует емкости. Так как модуль коэффициента отражения от нагрузки не изменяется вдоль ЛП, перемещение вдоль нее происходит вдоль дуги с постоянным радиусом, равным расстоянию от центра диаграммы до точки определяемой сопротивлением (проводимостью) нагрузки. При перемещении от нагрузки к источнику падающей волны (генератору) перемещение производится по часовой стрелке. Угол поворота радиуса равен 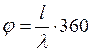. Здесь  - длина перемещения вдоль ЛП, - длина волны в ЛП.

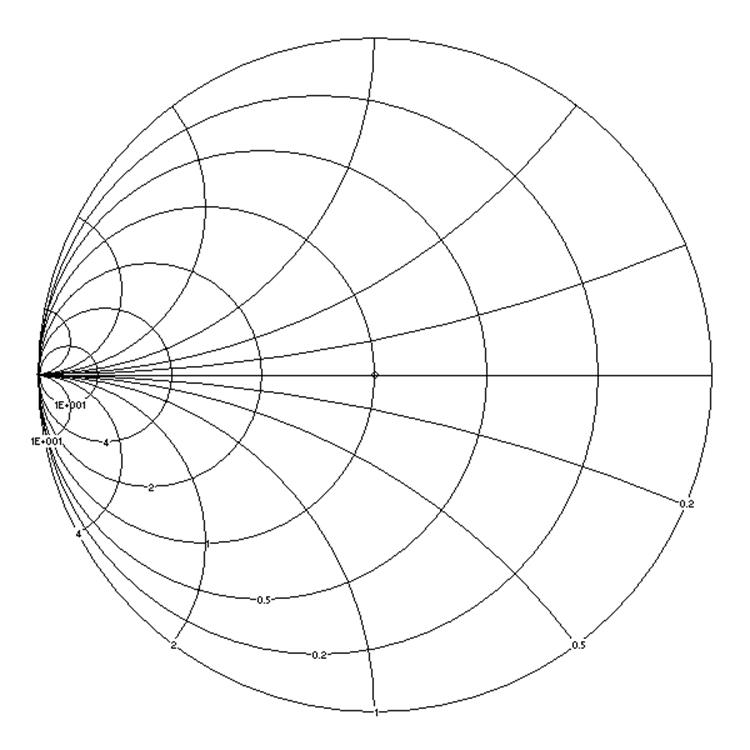
Рис. 1. Диаграмма  Вольперта – Смита для нормированных сопротивлений (проводимостей)

2. Порядок выполнения работы

Перейдем теперь к выполнению работы. В качестве нагрузки используются цепи RLC, резонансная частота которых лежит в области 1 ГГц. По указанию преподавателя бригада студентов получает одну из реализаций такой схемы, которую нужно согласовать с помощью одно-шлейфного согласования на частоте по указанию преподавателя. Далее открывается программа Microwave Office и в меню File выбираем New Project. Далее выбираем в меню Project/ Add Schematics/ New Schematics. В появившемся окне вводим название схемы – match, после чего появляется окно, в котором необходимо построить схему RLC цепи. В качестве примера рассмотрим цепь, схема которой изображена на рис. 2.

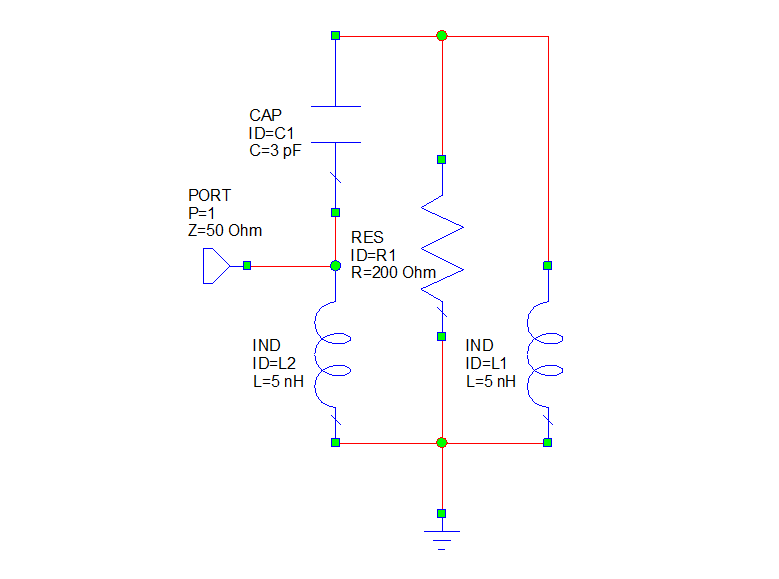
Рис. 2. Схема RLC цепи