Коаксиальная линия. Волны в направляющих структурах при произвольной нагрузке, страница 2

В безграничной регулярной линии можно представить себе одну бегущую (например, в сторону + z) волну:

,

,
но если линия заканчивается нагрузкой (рис. 2.1), то в общем случае падающая на нагрузку волна может полностью не поглотиться и тогда возникает характерное явление – отражение волны. Дело в том, что в бегущей волне напряжение и ток синфазны и их отношение равно волновому сопротивлению линии Z₀. На нагрузке же должен выполняться закон Ома и отношение комплексных амплитуд напряжения и тока должно определяться импедансом (комплексным полным сопротивлением) нагрузки Z_н. Появление отраженной волны обеспечивает выполнение закона Ома в сечении нагрузки:

;   ;   .                                                              (2.1)

Введем коэффициент отражения как отношение комплексных амплитуд напряжения отраженной и падающей волн

                                              .                                (2.2)

В сечении нагрузки из (2.1) получим

 или 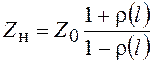. (2.3)

Итак, нагрузку линии передачи можно характеризовать как импедансом Z_н, так и комплексным коэффициентом отражения r_н.

Соотношение (2.2) позволяет определить коэффициент отражения r(z) в любом сечении линии. Модуль коэффициента отражения не меняется в зависимости от продольной координаты z, а фаза меняется линейно: . Аналогично (2.1) – (2.3) можно определить импеданс в любом сечении линии

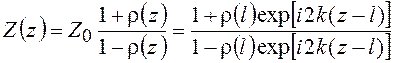,                        (2.4)
или после преобразований с учетом (2.3)

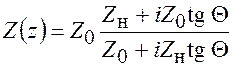                                          (2.5)
где Q = k(l – z) – электрическая длина отрезка l – z.

Соотношения (2.4) и (2.5) описывают так называемую трансформацию импеданса отрезком линии, когда импеданс в некотором сечении зависит от импеданса нагрузки, волнового сопротивления линии и от электрической длины отрезка. Разумеется, можно говорить и о входном сопротивлении (импедансе) отрезка линии Z_вх = Z(0). В общем случае Z_вх ¹ Z_н.

Если сопротивление нагрузки равно волновому сопротивлению линии (Z_н = Z₀ – согласованная нагрузка), то входное сопротивление при любой электрической длине отрезка неизменно и также равно волновому. Если электрическая длина отрезка кратна 180° (физическая длина кратна половине длины волны), то входное сопротивление равно сопротивлению нагрузки.

2.2. Суперпозиция падающей и отраженной волн

Монохроматические падающая и отраженная волны в линии суммируются – интерферируют. В линии формируется характерная картина смешанной волны – зависимость модуля амплитуды напряжения (или тока) от продольной координаты:

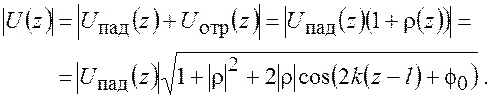
Эта зависимость периодическая с периодом l/2 . В ней чередуются максимумы и минимумы. Минимумы всегда несколько острее, чем максимумы. Рис. 2.2 иллюстрирует расчет коэффициента отражения, а также распределения напряжения и тока в линии при заданной нагрузке.

Отношение максимума и минимума в распределении напряжения (как и модуль коэффициента отражения) характеризует степень рассогласования нагрузки. Для описания режима работы линии используют коэффициент стоячей волны

                      ,       ,        (2.6)
и коэффициент бегущей волны    ().

Чем ближе к единице модуль коэффициента отражения, тем глубже минимумы. При полном отражении () формируется стоячая волна. В режиме стоячей волны энергия вдоль линии не передается и не поступает в нагрузку. Если же  (согласованная нагрузка, режим бегущей волны), то модули амплитуд напряжения и тока от продольной координаты не зависят, отраженной волны нет и вся энергия падающей волны рассеивается в нагрузке.

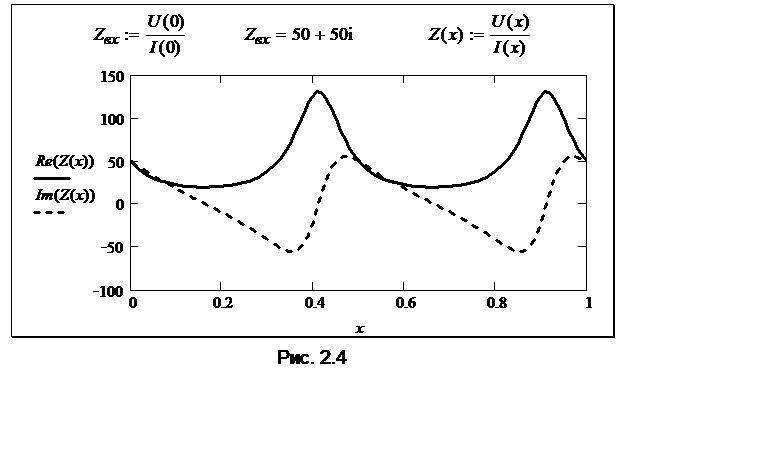Рис. 2.4 иллюстрирует описанную ранее трансформацию сопротивления в длинной линии – зависимость полного сопротивления линии от продольной координаты (по исходным данным, приведенным на рис. 2.2). Зависимость эта периодическая, как и следует из соотношений (2.3) и (2.4), с периодом l/2 . Чем меньше модуль коэффициента отражения (и КСВ), тем в меньших пределах трансформируется импеданс.