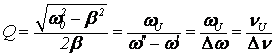 , (38)
, (38)
 4. Резонансные
характеристики контура можно использовать для определения параметров его
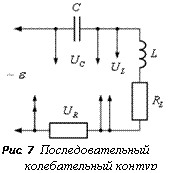
элементов. Реальный контур отличается от идеализированного (рис. 1) тем, что
катушка индуктивности L
имеет активное сопротивление RL
и, измеряя напряжение на катушке, мы тем самым измеряем суммарное падение
напряжения на индуктивности и активном сопротивлениях (рис. 7).
4. Резонансные
характеристики контура можно использовать для определения параметров его
элементов. Реальный контур отличается от идеализированного (рис. 1) тем, что
катушка индуктивности L
имеет активное сопротивление RL
и, измеряя напряжение на катушке, мы тем самым измеряем суммарное падение
напряжения на индуктивности и активном сопротивлениях (рис. 7).
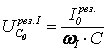 ,
, 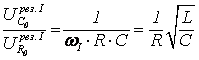 (41)
(41)
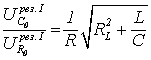 (42)
(42)
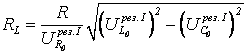 ,
(43)
,
(43)
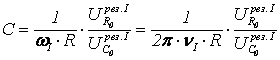 ,
(44)
,
(44)
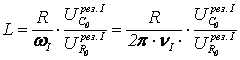 ,
(45)
,
(45)
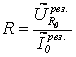 (46)
(46)
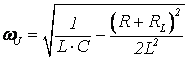 . (47)
. (47)
 (48)
(48)Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.