Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ»
кафедра физики
ИССЛЕДОВАНИЕ
ДИНАМИКИ ГАРМОНИЧСКИХ КОЛЕБАНИЙ
В ПОЛЕ СИЛЫ ТЯЖЕСТИ
Лабораторная работа № 2
РАБОТА 2
ИССЛЕДОВАНИЕ ДИНАМИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
В ПОЛЕ СИЛЫ ТЯЖЕСТИ
Цель работы: изучение закономерностей колебательного движения тела в однородном силовом поле; исследование процессов превращения энергии в консервативных системах; определение ускорения свободного падения.
Приборы и принадлежности: оборотный маятник; секундомер; масштабная линейка, чертежный треугольник.
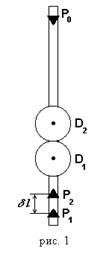 Конструкция оборотного
маятника представлена на рис. 1. На стержне 1 закреплены два диска – D1 и D2.
Маятник может быть подвешен на кронштейне с помощью легких призм P0, P1,
P2, трение в которых пренебрежимо
мало. Призма P0 является основной и
определяет положение оси вращения, маятник при этом качается с периодом Т0.
Положения призм P1 и P2 подобраны таким образом, что при подвешивании
маятника на этих призмах для периодов его качаний выполняется соотношение
Конструкция оборотного
маятника представлена на рис. 1. На стержне 1 закреплены два диска – D1 и D2.
Маятник может быть подвешен на кронштейне с помощью легких призм P0, P1,
P2, трение в которых пренебрежимо
мало. Призма P0 является основной и
определяет положение оси вращения, маятник при этом качается с периодом Т0.
Положения призм P1 и P2 подобраны таким образом, что при подвешивании
маятника на этих призмах для периодов его качаний выполняется соотношение
![]() .
.
Исследуемые закономерности.
Физический маятник. Тело, способное вращаться вокруг оси, проходящей выше его центра масс, совершает в поле тяготения гармонические колебания подобно математическому маятнику. В отличие от математического маятника качающееся тело произвольной формы называют физическим маятником. Выражение, определяющее период колебаний математического маятника,
![]()
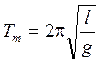 , (1)
, (1)
где l – длина подвеса математического маятника, g – ускорение свободного падения, оказывается справедливым для тела любой формы, поскольку для каждого тела, совершающего колебания в поле тяготения, можно найти математический маятник с таким же значением периода колебаний. В этом случае в выражении (1) используется приведенная длина физического маятника lпр, - величина, значение которой определяется распределением масс тела и взаимным расположением центра масс и оси вращения. Таким образом, для любого тела
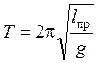 .
(2)
.
(2)
При небольших углах отклонения качающегося тела от положения равновесия справедливо выражение
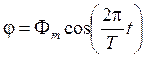 ,
(3)
,
(3)
где Фm – наибольший угол отклонения (амплитуда колебаний), а период колебаний Т определяется выражением (2).
Следовательно, качающееся тело произвольной формы можно представить математическим маятником, масса которого сосредоточена в точке, расположенной на расстоянии lпр от оси вращения. Эта точка называется центром качаний. Для центра качаний линейная скорость v и тангенциальное ускорение at легко определяются как, соответственно, первая и вторая производные по времени от (3), т.е.
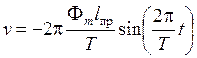 ,
(4)
,
(4)
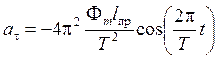 ,
(5)
,
(5)
Сосредоточив, условно, массу тела произвольной формы в центре качаний, можно наиболее простым образом провести анализ движения тела. В частности, из (4) и (5) получаются выражения, определяющие мгновенные значения кинетической и потенциальной энергии физического маятника
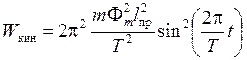 , (6)
, (6)
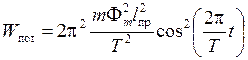 ,
(7)
,
(7)
Сложив выражения (6) и (7), делаем вывод о консервативном характере сил, действующих на качающееся тело. Действительно, полная энергия тела не зависит от времени, т.е. сохраняется.
Таким образом, математический маятник служит моделью любого тела, совершающего колебательное движение в поле тяготения около неподвижной оси. Формула (1) выражает универсальную закономерность, заключающуюся в том, что в поле тяготения период колебательного движения любого тела не зависит непосредственно от массы тела, а определяется исключительно значением ускорения свободного падения и характерным параметром, имеющим размерность длины.
Измерение ускорения свободного падения. Тот факт, что движение качающегося тела произвольной формы можно описать движением математического маятника соответствующей длины, позволяет провести измерение ускорения свободного падения. В принципе для этого достаточно знать приведенную длину маятника и измерить период его колебаний.
В данной работе используется иной способ, основанный на следующем свойстве центра качаний маятника, - если ось вращения перенести в центр качаний (обратить маятник), то период колебаний маятника не изменится. Называя в дальнейшем используемый в работе маятник оборотным, проведем обоснование методики измерений ускорения свободного падения.
Расстояние между осью вращения и центром качания l0 = lпр и определяет основной период колебания T0. Периоды колебаний маятника при подвешивании за призмы P1 и P2, соответственно, – T1 и T2 . Тогда периоды колебаний маятника при подвешивании за различные призмы могут быть рассчитаны как:
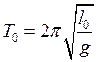 , (8)
, (8) 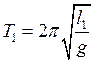 , (9)
, (9) 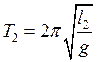 . (10)
. (10)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.