


















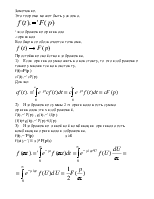















1. Задача о вычислении площади криволинейной трапеции. Интегральная сумма.
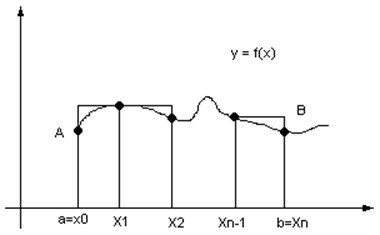
а = х0
S∆ (ABC)
Sn = ∑ Sпрямоуг = ∑ f(ti)(xi – xi-1) = ∑ f(ti) ∆xi .
![]()
∆xi → 0 .
Определенный интеграл
y = f(x) [a,b]
Разбиение отрезка [a,b]– совокупность точек xn.
xn ![]() [a,b]
[a,b]
х0 = a
хn = b
xi < xi+1
Рангом разбиения называется max ∆xi
∆xi = xi – xi-1.
Интегральная сумма f на отрезке [a,b] – называется сумма следующего вида
∑ f(ti) ∆xi , где ti ![]() [xi-1, xi]. xi –
точки разбиения отрезка.
[xi-1, xi]. xi –
точки разбиения отрезка.
Определенный интеграл функции f на отрезке [a, b] – предел интегральных сумм этой функции при условии, что этот предел не зависит ни от выбора разбиения ни от выбора точек ti (при стремлении ранга разбиения к 0).
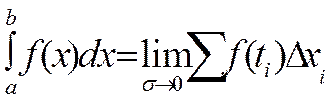 (Риман)
(Риман)
2. Определенный интеграл, его простейшие свойства. Достаточные условия интегрируемости.
Простейшие свойства:
1) Определенный интеграл от 0 функции равен 0
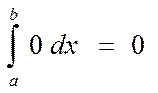
2) Определенный интеграл от 1, равен длине отрезка b-a
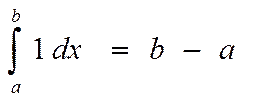
3) если верхний и нижний пределы совпадают, то результат равен 0.
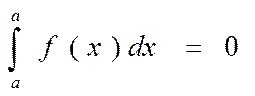
4)
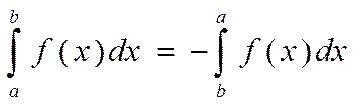
Функция Дирихле.
Она равна 0 в иррациональных точках и равна 1 в рациональных точках.
Если функция задана на отрезке и имеет заданное число точек разрыва, то у нее существует определенный интеграл.
Функция, имеющая на данном отрезке определенный интеграл, называется интегрируемая.
3. Свойства определенного интеграла, выражаемые равенствами.
1) постоянный множитель можно выносить
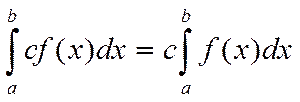
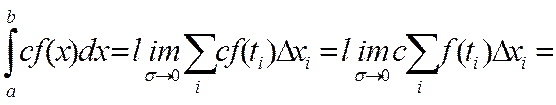
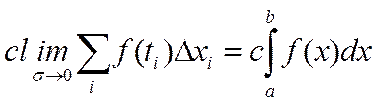
2) Определенный интеграл от суммы двух функций равен сумме двух функций
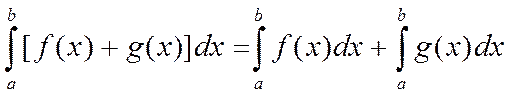
Док- во
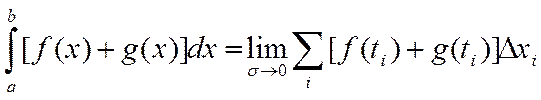
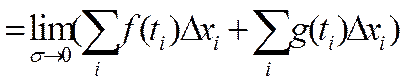 по свойству предела
по свойству предела
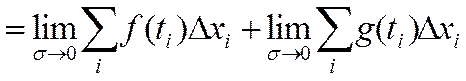
3) Определенный интеграл от линейной комбинации двух функций равен линейной комбинации интегралов.
 по свойству 2 имеем:
по свойству 2 имеем:
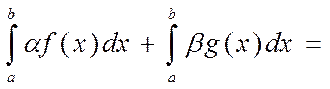 по свойству 1 имеем:
по свойству 1 имеем:
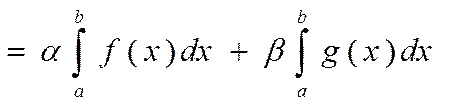
Замечание: по индукции это свойство можно распространить на любое число функций.
3) Аддитивность
[a, b] c - внутри отрезка

Определение интеграла
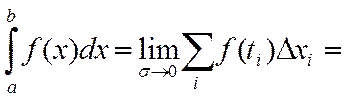 любые разбиения.
любые разбиения.
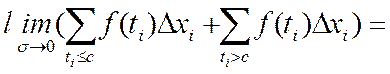
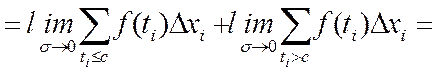
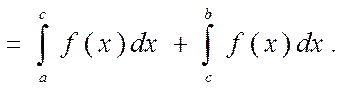
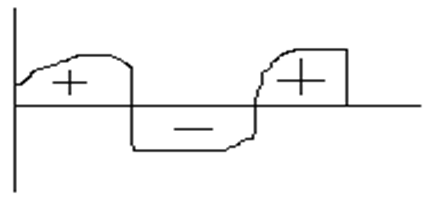
Характеристические свойства:
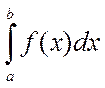 , равен
алгебраической сумме образованной осью абсцисс и графиком функции (выше оси
абсцисс «+», ниже «-»).
, равен
алгебраической сумме образованной осью абсцисс и графиком функции (выше оси
абсцисс «+», ниже «-»).
4. Свойства определенного интеграла, выражаемые неравенствами.
1о) Если f(x)≥0 на [a, b], то
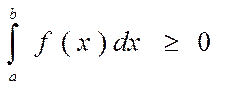
Доказательство:
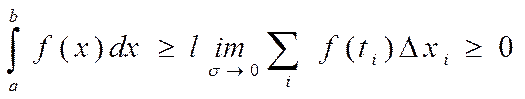 ,
где
,
где
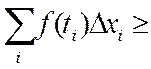 0,
0, 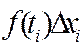 ≥0,
≥0, 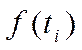 ≥0,
≥0, 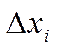 >0.
>0.
2о) Если на [a, b] выполняется f(x)≤g(x), то
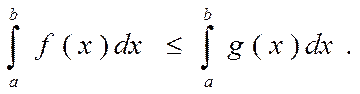
Доказательство:
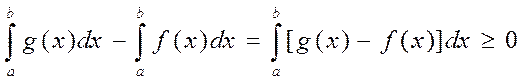 ,
,
где 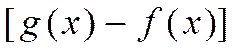 ≥0.
≥0.
3о) Если функция f(x) интегрируема на отрезке [a, b], то выполняется неравенство:
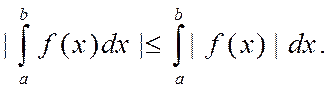
Доказательство:
-z≤y≤z ![]() |y|≤z.
|y|≤z.
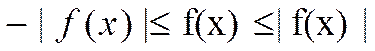
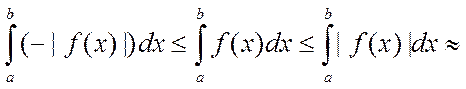
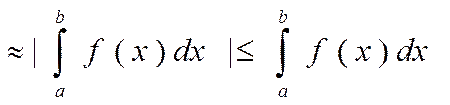 .
.
5. Теорема о среднем значении.
Для
непрерывной на отрезке [a,b] функции f существует точка 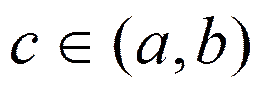 такая, что
такая, что 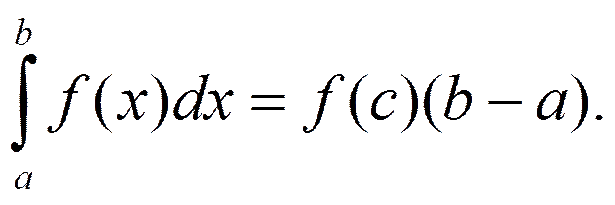
Так
как f непрерывна, то для
неё существует первообразная Ф, поэтому 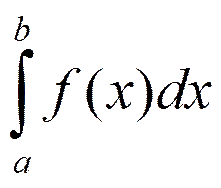 =
|формула Ньютона-Лейбница для непрерывной на [a,b] функции f| =
=
|формула Ньютона-Лейбница для непрерывной на [a,b] функции f| = 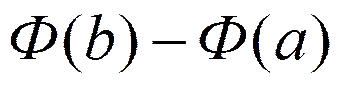 = |формула Лагранжа для Ф| =
= |формула Лагранжа для Ф| = 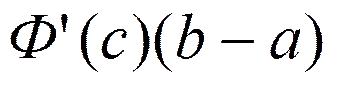 = |так как
= |так как 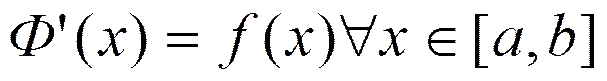 | =
| = 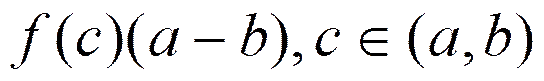
6. Интеграл с переменным верхним пределом. Теорема Барроу.
Пусть
функция f кусочно-непрерывна
на [a,b]. Функция 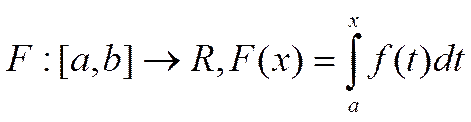 называется интегралом с переменным верхним
пределом.
называется интегралом с переменным верхним
пределом.
Теорема
Барроу. Пусть ![]() – точка непрерывности функции f, тогда
– точка непрерывности функции f, тогда 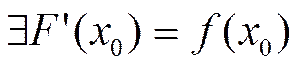 , иначе
, иначе 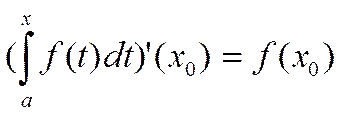 . Так
как f кусочно-непрерывна
и
. Так
как f кусочно-непрерывна
и ![]() - точка непрерывности функции f, то можно выбрать
- точка непрерывности функции f, то можно выбрать ![]() так, что на интервале
так, что на интервале 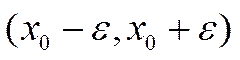 функция f будет непрерывна.
Возьмём произвольное
функция f будет непрерывна.
Возьмём произвольное 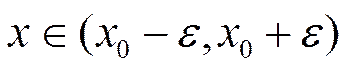 . По теореме о среднем значении
. По теореме о среднем значении 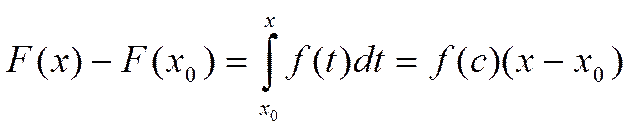 , где c лежит между x и
, где c лежит между x и ![]() . По теореме о пределе сжатой функции
. По теореме о пределе сжатой функции 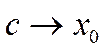 при
при 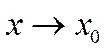 и,
следовательно,
и,
следовательно, 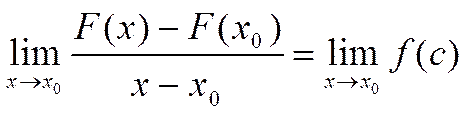 =
= 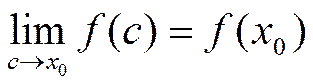 .
Значит,
.
Значит, 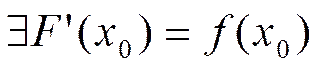 . Через <a,b> будем
обозначать промежуток, когда он может быть открытым или замкнутым, при этом a может равняться
. Через <a,b> будем
обозначать промежуток, когда он может быть открытым или замкнутым, при этом a может равняться ![]() , а b может равняться
, а b может равняться ![]() .
.
7. Теорема Ньютона-Лейбница.
Если
F(x) есть какая-либо
первообразная от непрерывной функции f(x), то справедлива формула 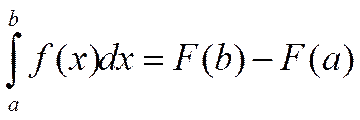 (формула Ньютона-Лейбница).
(формула Ньютона-Лейбница).
Пусть
F(x) есть некоторая
первообразная от функции f(x). По теореме о производной от
определенного интеграла по верхнему пределу функция 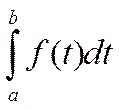 есть
также первообразная от f(x). Но две любые первообразные от данной
функции отличаются на постоянное слагаемое C*. Следовательно,
можно написать:
есть
также первообразная от f(x). Но две любые первообразные от данной
функции отличаются на постоянное слагаемое C*. Следовательно,
можно написать: 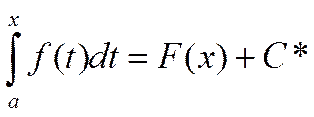 . Это равенство при
соответствующем выборе C* справедливо при всех значениях x, т. е. является
тождеством. Для определения постоянного C* положим в этом
тождестве x=a; тогда
. Это равенство при
соответствующем выборе C* справедливо при всех значениях x, т. е. является
тождеством. Для определения постоянного C* положим в этом
тождестве x=a; тогда 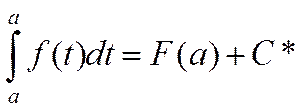 , или
, или ![]() ,
откуда
,
откуда ![]() . Следовательно,
. Следовательно, 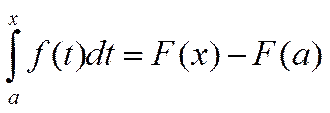 .
Полагая x=b, получим формулу
Ньютона-Лейбница:
.
Полагая x=b, получим формулу
Ньютона-Лейбница: 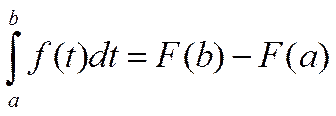 , или, заменив обозначение
переменной интегрирования на x:
, или, заменив обозначение
переменной интегрирования на x: 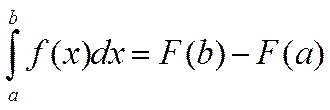 .
Разность F(b)-F(a) не зависит от
выбора первообразной F, так как все первообразные отличаются на
постоянную величину, которая при вычитании всё равно уничтожается.
.
Разность F(b)-F(a) не зависит от
выбора первообразной F, так как все первообразные отличаются на
постоянную величину, которая при вычитании всё равно уничтожается.
8. Интегрирование по частям в определенном интеграле.
Если
функции u и v непрерывно
дифференцируемы на [a,b], то справедливо
равенство 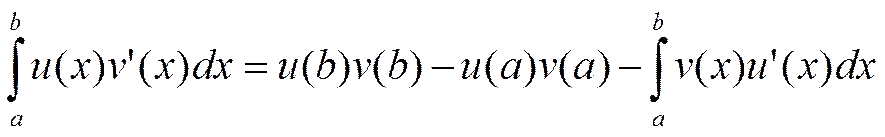 .
.
Как
известно, 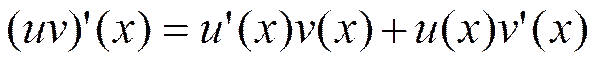 . Все входящие в равенство функции
непрерывны, а значит, и интегрируемы на [a,b]. Функция uv – первообразная к
(uv)’ на [a,b]. Тогда по теореме
Ньютона-Лейбница и теореме о линейности интеграла
. Все входящие в равенство функции
непрерывны, а значит, и интегрируемы на [a,b]. Функция uv – первообразная к
(uv)’ на [a,b]. Тогда по теореме
Ньютона-Лейбница и теореме о линейности интеграла 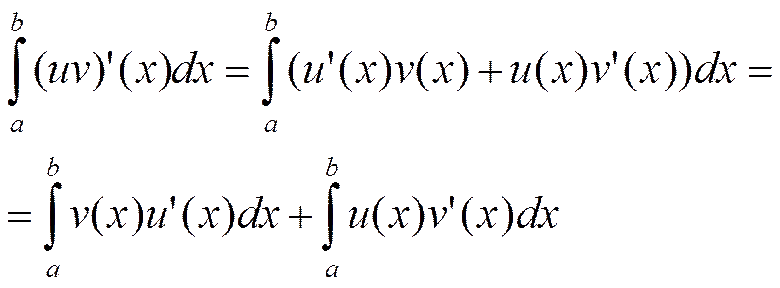 и
и 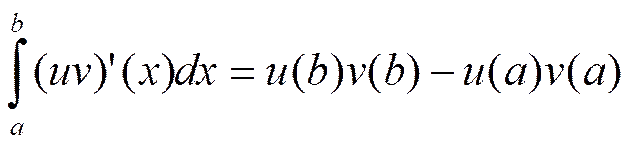 . Следовательно,
. Следовательно, 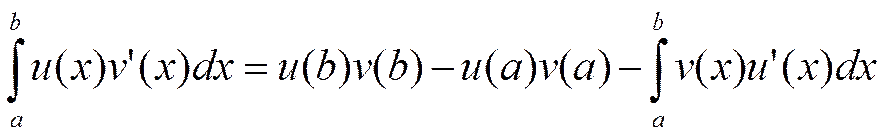
9. Замена переменной в определенном интеграле.
Пусть для вычисления
интеграла 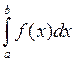 сделана подстановка
сделана подстановка ![]() .
.
Теорема: если:
1) функция ![]() и ее производная
и ее производная ![]() непрерывна при
непрерывна при ![]() ;
;
2) множеством значений функции ![]() при
при
![]() является отрезок [a;b];
является отрезок [a;b];
3) ![]() и
и ![]() , то
, то
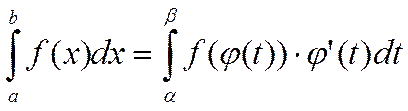 (1)
(1)
доказательство:
пусть F(x) есть первообразная для f(x) на
отрезке [a;b]. Тогда по формуле Ньютона-Лейбница 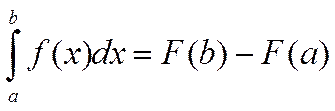 . Так как
. Так как ![]() то
то ![]() является первообразной для функции
является первообразной для функции ![]() ,
, ![]() .
Поэтому по формуле Ньютона-Лейбница имеем :
.
Поэтому по формуле Ньютона-Лейбница имеем : 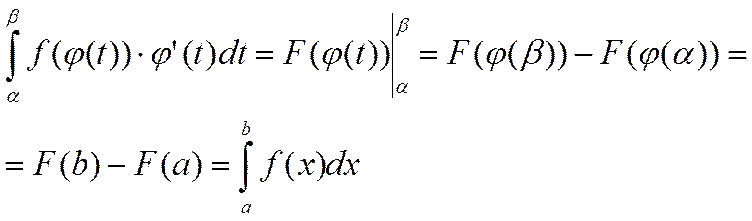 формула
(1) называется формулой замены переменной в определенном интеграле.
формула
(1) называется формулой замены переменной в определенном интеграле.
Отметим, что:
1) при вычислении определенного интеграла методом подстановки (замена переменной) возвращаться к старой переменной не требуется;
2) часто вместо подстановки ![]() применяют
подстановку
применяют
подстановку ![]() ;
;
3) не следует забывать менять пределы интегрирования при замене переменных.
10. Несобственные интегралы 1-го рода.
Пусть
функция ![]() непрерывна на промежутке
непрерывна на промежутке ![]() . По определению несобственный интеграл
1-го рода :
. По определению несобственный интеграл
1-го рода :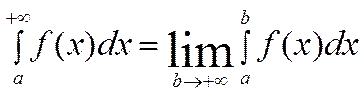
Если
существует конечный предел 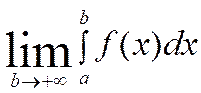 , несобственный
интеграл 1-го рода
, несобственный
интеграл 1-го рода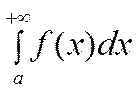 сходится .
сходится .
Если
же указанный предел не существует или он бесконечен, то говорят что интеграл 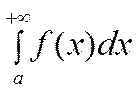 расходится.
расходится.
Аналогично
определяется несобственный интеграл на промежутке ![]() :
:
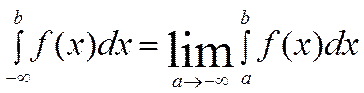 .
.
Несобственный интеграл с двумя бесконечными пределами определяется формулой:
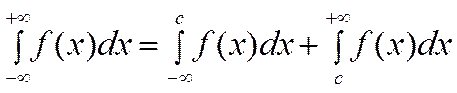 , где с – произвольное число.
, где с – произвольное число.
В этом случае интеграл слева сходится лишь тогда когда сходятся оба интеграла справа.
Если
![]() на промежутке
на промежутке ![]() и
интеграл
и
интеграл 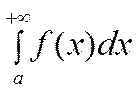 сходится, то он выражает площадь
бесконечно длинной криволинейной трапеции.
сходится, то он выражает площадь
бесконечно длинной криволинейной трапеции.
Несобственные интегралы 2-го рода.
Пусть
функция ![]() непрерывна на промежутке [a;b) и
имеет бесконечный разрыв при x=b. По определению несобственный интеграл 1-го рода:
непрерывна на промежутке [a;b) и
имеет бесконечный разрыв при x=b. По определению несобственный интеграл 1-го рода: 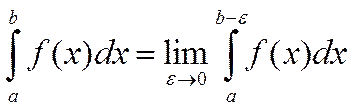
если
существует конечный предел 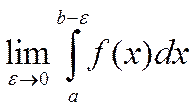 несобственным
интегралом второго рода
несобственным
интегралом второго рода 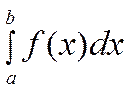 сходится. Если же
указанный предел не существует или бесконечен – то интеграл
сходится. Если же
указанный предел не существует или бесконечен – то интеграл 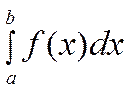 расходится.
расходится.
Аналогично
если функция ![]() терпит бесконечный разрыв в точке x=a, то
полагают :
терпит бесконечный разрыв в точке x=a, то
полагают : 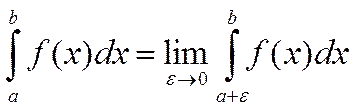 .
.
Если
функция ![]() терпит разрыв во внутренней точке cотрезка
[a;b], то несобственный интеграл второго рода определяется
формулой:
терпит разрыв во внутренней точке cотрезка
[a;b], то несобственный интеграл второго рода определяется
формулой: 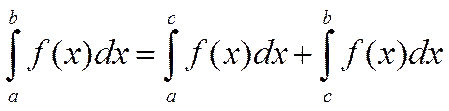 ; в этом случае интеграл слева называют
сходящимся, если оба несобственных интеграла, стоящих справа, сходятся.
; в этом случае интеграл слева называют
сходящимся, если оба несобственных интеграла, стоящих справа, сходятся.
В
случае если ![]() несобст. интеграл 2-го рода
несобст. интеграл 2-го рода 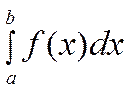 (разрыв в точке x=b)
можно истолковать геометрически как площадь бесконечно высокой криволинейной
трапеции.
(разрыв в точке x=b)
можно истолковать геометрически как площадь бесконечно высокой криволинейной
трапеции.
11. Теоремы сравнения для несобственных интегралов (НИ).
пусть
![]() :
:
1) первый признак сравнения НИ.
Если
![]() ,
, ![]() , то
, то
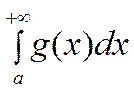 - сход =>
- сход => 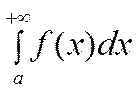 - сход.
- сход.
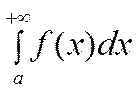 -расх. =>
-расх. => 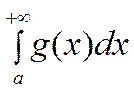 - расх.
- расх.
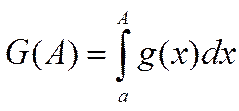 ,
, 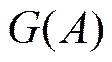 -
возрастающая ф-ия
-
возрастающая ф-ия
А<A’
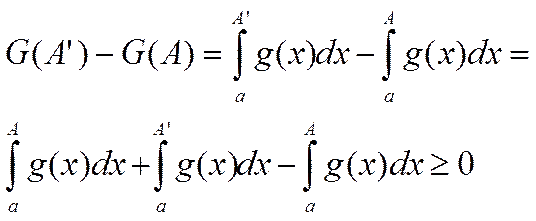
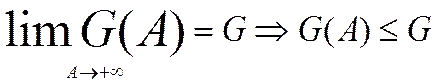
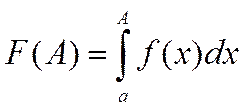
![]() - возвр. ;
- возвр. ; ![]() - огр-я,
т.к.
- огр-я,
т.к. ![]()
сущ-ет
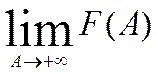
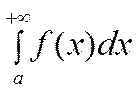 -расх. =>
-расх. => 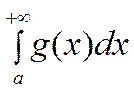 - расх.
- расх.
2) второй признак сравнения
![]() ,
, ![]()
если
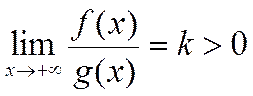 , то
, то 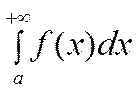 и
и 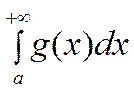 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Док-во:
![]()
![]() ,
, ![]() ,
, 
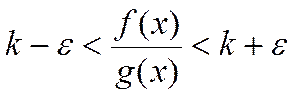
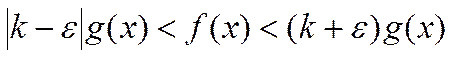
пусть
![]()
![]()
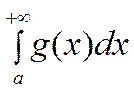 - сходится при
- сходится при ![]()
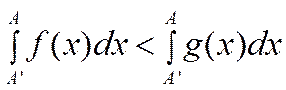
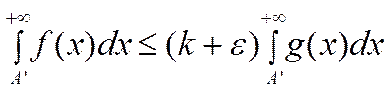
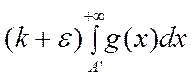 - сход. =>
- сход. => 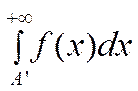 -
сход-ся
-
сход-ся
аналогично расхождение.
12. Сходимость интегралов вида:
А)
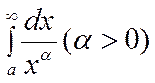 ;
; 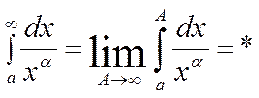
I) ![]()
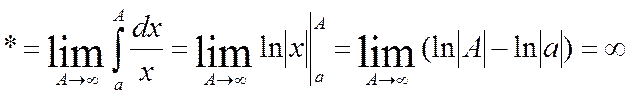 => расх.
=> расх.
II) ![]()
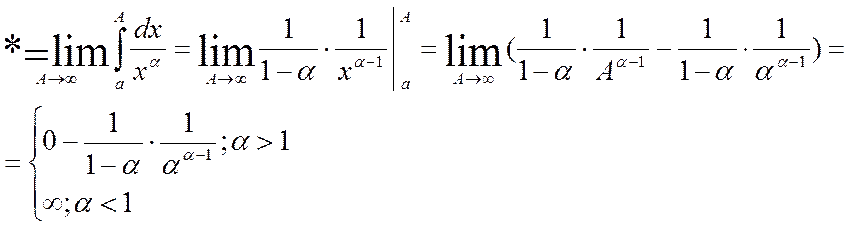
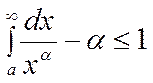 - расх. ;
- расх. ; 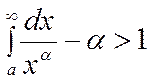 - сход.
- сход.
Замечание : если ![]() на
на ![]() , то
, то ![]() на
на ![]() ;
; ![]()
Б)
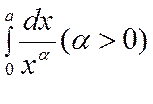 ; где α – постоянное число, имеет
единственную особенность в точке х=0, чтобы выяснить сходится ли он, надо
вычислить предел
; где α – постоянное число, имеет
единственную особенность в точке х=0, чтобы выяснить сходится ли он, надо
вычислить предел
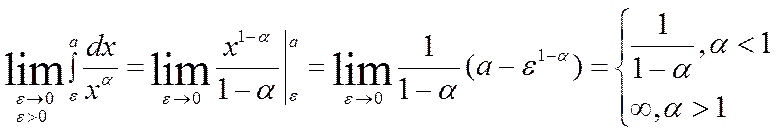
таким
образом интеграл 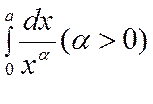 сходится при
сходится при ![]() и равен
и равен ![]() ; и
расходится при
; и
расходится при ![]() . если же
. если же ![]() ,
то он расходится:
,
то он расходится:
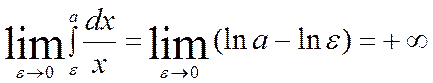
13. Абсолютная сходимость несобственных интегралов . Теорема об абсолютной сходимости для несобственных интегралов 1-го (2-го) рода.
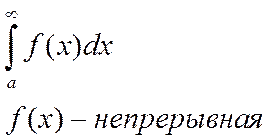
Теорема об абсолютной сходимости интегралов это следствие о несобственном интеграле (для того чтобы интеграл был несобственным необходимо и достаточно чтобы для любого ε>0 нашлось такое бε>0 , которое обладало бы следующим свойством:
Если числа А и А’> бε
(бε <А<A’) , то 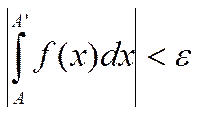 ).
).
Теорема об абсолютной сходимости интегралов.
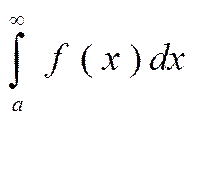 Несобственный интеграл наз-ся абсолютно сходящимся
если сходится несобственный интеграл:
Несобственный интеграл наз-ся абсолютно сходящимся
если сходится несобственный интеграл: 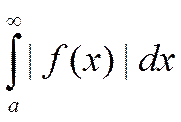 . При этом f(x)
называется абсолютно интегрируемой функцией.
. При этом f(x)
называется абсолютно интегрируемой функцией.
Теорема. Если несобственный интеграл сходится абсолютно, то он сходится и в обычном смысле.
Док-во.
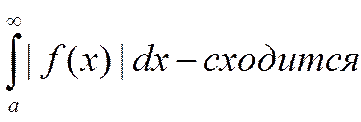
Воспользуемся критерием сходимости несобств. интегралов. Найдется такое бε>0, что А’>A> бε и выполняется неравенство:
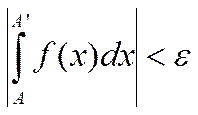
зададим ε>0
 по известному св-ву неравенств от интегралов
по известному св-ву неравенств от интегралов
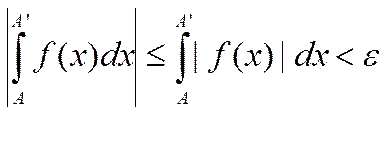 для всякого ε>0 существует бε ,
такое что
для всякого ε>0 существует бε ,
такое что
А’>A> бε . Следовательно теорема доказана.
14. Две теоремы о сходимости несобственных интегралов 1-го (2-го) рода от знакопеременных функций.
Теорема 1.
Если мы рассмотрим несобственный интеграл:
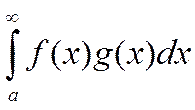
и ф-ции f(x) и g(x) удовлетворяют следующему условиям:
1) А>0
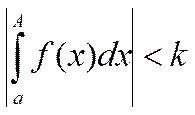
2) g(x) явл-ся монотонной и дифференцируемой функцией
3) 
Тогда исходный несобственный интеграл сходится.
Теорема 2. О сходимости несобственных интегралов.
f(x), g(x) [a,∞)
функция g(x) дифференцируема
1. Интеграл Лапласа. Оригиналы и изображения, их простейшие свойства.
Основные понятия.
f(t)
f:R→C
1) Ф-ция f(t) предполагается непрерывной и n раз дифференцируемой за исключением некоторого числа точек, в которых ф-ция и её производные имеет разрывы 1-го рода. Эти точки являются изомерными.
2) |f(t)| удовлетворяет неравенству:
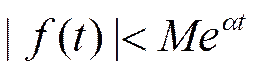
α-показатель роста f(t)
3) 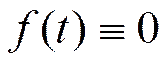
если t<0
f(t)=U(t)+iv(t)
f’(t)=U’(t)+iv’(t)
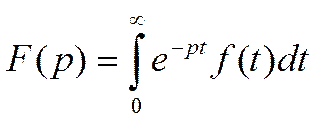 Интеграл Лапласа
Интеграл Лапласа
Ф-ция F(p) определена [0,∞) наз-ся изображением ф-ции f(t)
p=σ+iρ
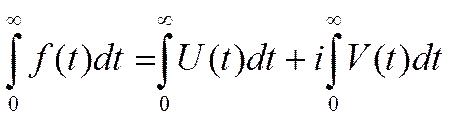
f(t)- если обладает свойствами оригинала, то F(p) определена в комплексной полуплоскости, у которых вещественная часть р больше α.
Rep>α , то F(p)-бесконечно диффир. ф-ция.
Замечание.
Эта теорема может быть усилена.
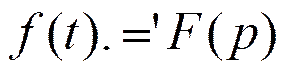
‘-изображение оригинала
.-оригинал
Вообще все обозначается точками.
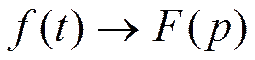
Простейшие свойства изображения.
1) Если оригинал умножить на константу, то его изображение также умножится на константу.
f(t)=F(p)
cf(t).=’cF(p)
Док-во:
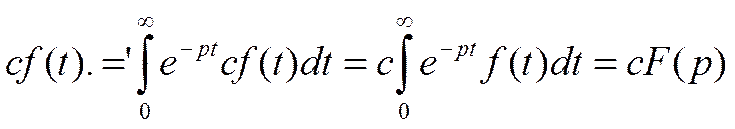
2) Изображение суммы 2-ч оригиналов есть сумма оригиналов этих изображений.
f(t).=’F(p) , g(t).=’G(p)
(f(t)+g(t)).=’F(p)+G(p)
3) Изображение линейной комбинации оригинала есть комбинация оригинала изображения.
f(t).=’F(p) α>0
f(αt).=’(1/ α)*F(p/α)
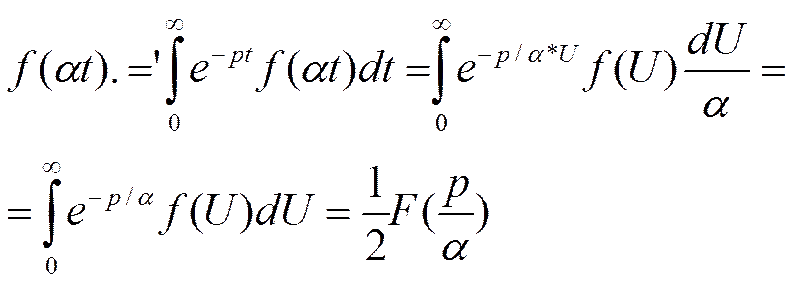
2) Дифференцирование оригиналов и изображений
Теорема о дифференцировании оригинала: Если f(t) имеет изображение F(p) то f’(t) имеет изображение
pF(p)-f(0)
Д-во:
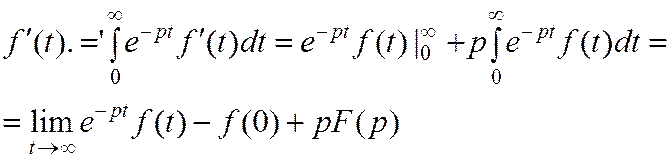
Докажем, что 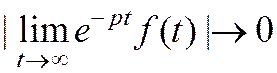
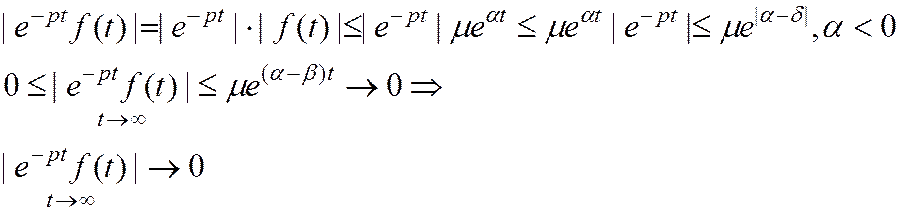
Замечание:
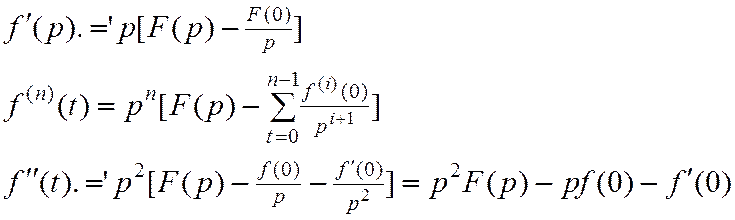
Теорема о дифференцировании изображения:
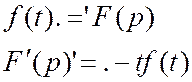
Док-во:
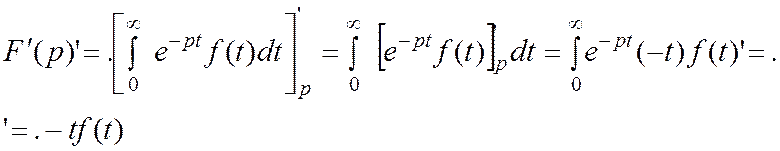
Замечание: 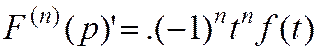
3)Интегрирование оригиналов и изображений.
Теорема об интегрировании оригинала:
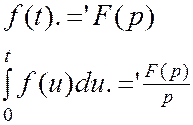
Док-во:
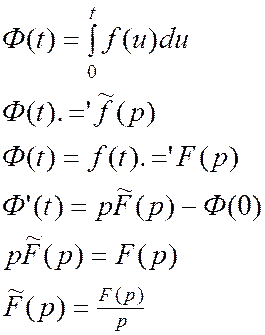 По
т.о диффер. изображений
По
т.о диффер. изображений
Теорема об интегрировании изображений:
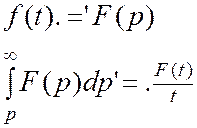
Док-во:
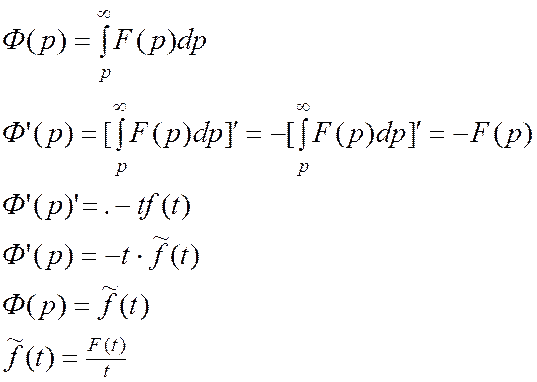 По
т.о дифф.ориг
По
т.о дифф.ориг
4) Теоремы затухания, запаздывания, опережения.
Теорема запаздывания (свойство сдвига)
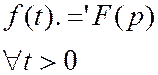
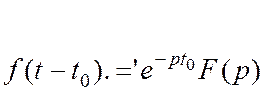
Доказательство:
![]() тогда
тогда 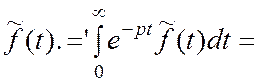
Заметим что![]() , если
t<t0 (из определения
, если
t<t0 (из определения ![]() )
)
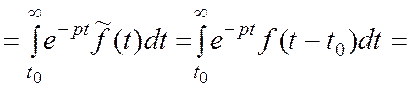
Пусть t – t0= u
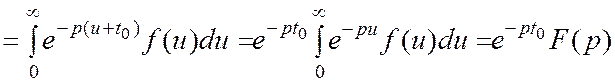
Теорема затухания
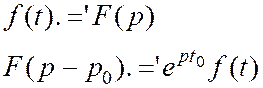
Доказательство:
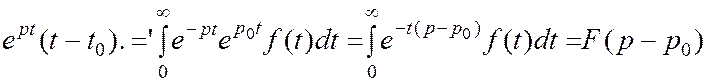
Теорема опережения:
![]()
![]()
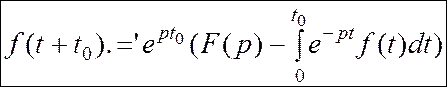 Доказательство:
Доказательство: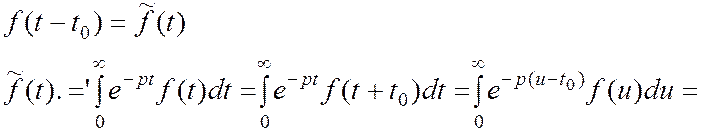
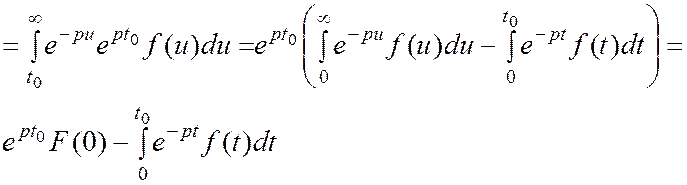
5) Решение дифференциальных уравнений операционным методом
Основные определения теории дифференциальных уравнений
(О)Уравнение содержащее неизвестную функцию и её производную называется обыкновенным дифференциальным уравнением
F(x, y, y’,…,y(n))=0
(О)Порядок старшей производной, входящей в состав уравнения, называется порядком дифференциального уравнения
(О)Решением дифференциального уравнения наз-ся функция, определенная на <a,b>, которая при подстановке в дифференциальное уравнение обращает его в тождество.
Решения должны быть на сплошном промежутке
(О)Процесс отыскания решения дифференциального уравнения наз-ся интегрированием дифференциального уравнения
(О)График решения дифференциального наз-ся интегральной прямой
(О)Если дифференциальное уравнение разрешимо относительно старшей производной то такая форма ДУ наз-ся нормальной
g(n)=f(x, y, y’,…,y(n))
y’=f(x)
![]()
Если уравнение первого порядка то его решение y=y(x,c)
Если уравнение второго порядка то его решение y=y(x,c1,c2) и т.д.
Часть ДУ первого порядка:
F(x, y, y’)=0 y(x0)=y0
Часть ДУ второго порядка:
F(x, y, y’, y’’)=0
Через (x0,y0) проходит бесконечно много решений, тогда
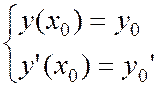 решения
определяются единственным образом
решения
определяются единственным образом
Для ДУ n-го порядка
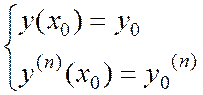
![]() ,
y(0)=0, y’(0)=1
,
y(0)=0, y’(0)=1
Приведем в изображение обе части:
Левая часть:
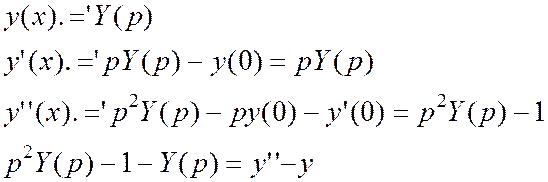
Правая часть:
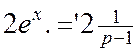
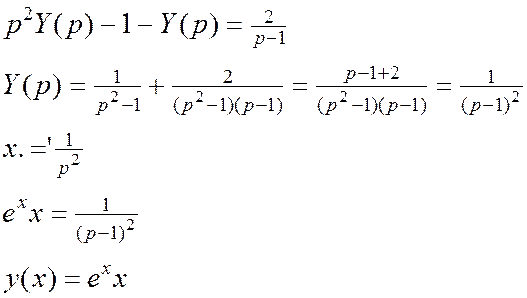
Функции многих переменных.
Билет №1: Предел и непрерывность функций нескольких переменных.
Предел.
Пусть функция z=f(x;y) определена в некоторой точке окрестности точки М0(xo;yo), кроме быть может, самой этой точки. Число А называется пределом функции z=f(x;y) при x →xo и y→yo, если для любого ε>0 существует δ>0 такое, что для всех x≠xo и y≠yo и удовлетворяющих неравентству √((x-xo)2+(y-yo)2)<δ выполняется неравенство |f(x;y)-A|<ε. Записывают: A=lim f(x;y) ; при пределе стремящемся: x к xo и y к yo. Из определения следует, что если предел существует, то он не зависит от пути, по которому М стремится к М0. Геометрический смысл предела функции двух переменных состоит в том: каково бы ни было число ε>0, найдется δ-окрестность точки М0(хо;уо), что во всех ее точках М(х;у), отличных от М0, аппликаты соответствующих точек поверхности z=f(x;y) отличаются от числа А по модулю меньше, чем на ε. Предел функции многих переменных обладает свойствами, аналогичными свойствам предела функции одной переменной. Если функции f(M) и g(M) определены на множестве D и имеют в точке М0 этого множества пределы А и В соответственно, то и функции f(M)±g(M), f(M)*g(M), f(M)/g(M) (g(M)≠0) имеют в точке М0 пределы , которые соответственно равны А±В, А*В, А/В (В≠0). Свойства:
1. Функция может иметь только один предел при х→хо и у→уо.
2. Постоянный множитель можно выносить за знак предела.
3. Предел степени с натуральным показателем равен той же степени предела.
Непрерывность.
Функция z=f(x;y) называется непрерывной в точке М0(хо;уо), если она:
1. Определена в этой точке и некоторой ее окрестности,
2. Имеет предел lim f(M) (при пределе стремящимся М→М0),
3. Этот предел равен значению функции z в точке М0, т.е.
lim f(M)=f(M0) или lim f(x;y)=f(xo;yo) при х→хо и у→уо.
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается (не выполняется хотя бы одно из условий непрерывности функций в точке), называются точками разрыва функции. Точки разрыва z=f(x;y) могут образовывать целые линии разрыва. Можно дать другое определение непрерывности функции z=f(x;y) в точке. Обозначим ∆х=х-хо, ∆у=у-уо, ∆z=f(x;y)-f(xo;yo). Величины ∆х и ∆у называются приращениями аргументов х и у, а ∆z- полным приращением функции f(x;y) в точке М0(хо;уо). Функция z=(x;y) называется непрерывной в точке М0(хо;уо)€D если выполняется равентсво lim ∆z=0 (∆x→0,∆y→0), т.е. полное приращение функции в этой точке стремится к нулю, когда приращения ее аргументов х и у стремятся к нулю.
Билет №2: Частные производные и дифференциалы.
Пусть задана функция z=f(x;y). Так как х и у – независимые переменные, то одна из них может изменяться , а другая сохранять свое значение. Дадим независимой переменной х приращение ∆х, сохраняя значение у неизменным. Тогда z получит приращение, которое называется приращением z по х и обозначается ∆xz. ∆xz=f(x+∆x;y)-f(x;y). Аналогично получаем частное приращение z по у: ∆уz=f(x;y+∆y)-f(x;y). Полное приращение ∆z для функции z определяется равенством: ∆z=f(x+∆x;y+∆y)-f(x;y).
Если существует предел: lim ((∆xz)/(∆x))=lim (f(x+∆x;y)-f(x;y))/(∆x) –при ∆х→0, то он называется частной производной функции z=f(x;y) в точке М(х;у) по переменной х и обозначается одним из символов: z’x, ∂z/∂x, fx’, ∂f/∂x. Аналогично определяется и обозначается частная производная от z=f(x;y) по переменной у: z’x=lim ∆yz/∆y=lim (f(x;y+∆y)-f(x;y))/∆y –при ∆у→0. Таким образом, частная производная функции нескольких переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции f(x;y) находят по формулам и правилам вычисления производных функций одной переменной, при этом х или у считается постоянной величиной.
Билет №3: Полный дифференциал и дифференцируемость функции
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.