В работу могут быть включены очень простые задачи (например, см. 36-40). Числа в задачах могут быть любыми.
36. СВ равновероятно принимает значения +1 или -2. Найти ее математическое ожидание и дисперсию.
37. СВ имеет равномерную ПВ в интервале [-1; 3]. Найти ее математическое ожидание, медиану, квартили и дисперсию.
38. СВ принимает значения +1 или -1. Вероятность значения +1 равна 0,4. Записать и построить ПВ и ФР этой СВ.
39. СВ Х имеет равномерную ПВ в интервале [-1; 3]. Построить ПВ и ФР для СВ Y = 2X-1.
40. СВ Х имеет нормальную ПВ с математическим ожиданием 2 и дисперсией 4. Записать ПВ и ФР случайной величины Y = 3X+8.
41. Дать определение случайной функции, случайного процесса. Какие характеристики дают полное вероятностное описание СП? Запишите математические выражения для этих характеристик.
42. Приведите классификацию случайных процессов в зависимости от характера области определения и области значения СП.
43. Какие характеристики дают полное статистическое описание СП?
44. Записать
выражения для математического ожидания, дисперсии и корреляционной функции произвольного
СП. Верно ли равенство ![]() =
=![]() ?
?
45. Как
определяется взаимная корреляционная функция СП ![]() и
и ![]() ?
?
46. Дать определение СП с независимыми отсчетами, марковского СП, СП с независимыми приращениями.
47. Дать определение СП, стационарного в широком и узком смыслах.
48. Дать определение эргодического СП. Как для эргодического СП определить математическое ожидание и корреляционную функцию путем усреднения по времени?
49. Что называется квазидетерминированным СП? Привести примеры.
50. Как связаны между собой корреляционная функция и спектральная плотность стационарного СП? Перечислить свойства корреляционной функции и спектральной плотности стационарного СП.
51. Сформулируйте теорему Винера-Хинчина. Как, зная спектральную плотность стационарного СП, найти его дисперсию?
52. Доказать
утверждения: ![]() =D;
=D; ![]() .
.
53. Как определяется время корреляции и эффективная ширина спектра для стационарного СП? Сформулировать соотношение неопределенности для стационарного СП.
54. Какой
процесс называют «белым» шумом? Какой вид имеют ![]() и
и ![]() для данного процесса?
для данного процесса?
55. Какой
процесс называют финитным «белым» шумом? Какой вид имеют ![]() и
и ![]() для данного
процесса?
для данного
процесса?
56. Дать
определение узкополосного процесса. Какой вид в общем случае имеет КФ
узкополосного СП? При каких условиях КФ узкополосного СП имеет вид ![]() ?
?
57. Какой
вид имеет ![]() стационарного СП с дискретным энергетическим
спектром?
стационарного СП с дискретным энергетическим
спектром?
58. Чему равна корреляционная функция линейной комбинации независимых центрированных случайных процессов? Ответ аргументировать.
59. Чему равна спектральная плотность суммы независимых центрированных стационарных случайных процессов?
60. Что такое телеграфный сигнал? Какой вид имеет его КФ?
61. Дать определение непрерывности СП в точке.
62. Сформулировать необходимые и достаточные условия дифференцируемости СП.
63. Дать определение нормального СП.
64. Дать определение винеровского процесса. Является ли этот процесс стационарным?
65. Дать определение узкополосного нормального СП.
66. Как определяется комплексная огибающая СП? Какие свойства имеет огибающая (комплексная огибающая) СП?
67. Записать квадратурное представление узкополосного СП.
68. Какие
статистические характеристики имеют амплитуды квадратурных составляющих ![]() и
и ![]() для
узкополосного нормального СП?
для
узкополосного нормального СП?
69. Какой
будет совместная ПВ огибающей ![]() и фазы
и фазы ![]() узкополосного нормального СП? Будут ли
узкополосного нормального СП? Будут ли ![]() и
и ![]() зависимыми
СВ? Как изменится ситуация при добавлении к узкополосному нормальному СП
гармонического сигнала
зависимыми
СВ? Как изменится ситуация при добавлении к узкополосному нормальному СП
гармонического сигнала ![]() , где
, где ![]() – центральная частота энергетического
спектра СП?
– центральная частота энергетического
спектра СП?
70. Что такое функционал плотности вероятности нормального СП?
71. Как выглядит ФПВ для нормального «белого» шума? Как зависит «вероятность» отдельной реализации нормального «белого» шума от ее энергии?
72. Дать определение марковского процесса. Приведите пример марковского процесса.
73. Дать определение стационарной линейной системы.
74. Что такое импульсная характеристика и коэффициент передачи стационарной линейной системы? Как эти понятия связаны между собой?
75. Как найти математическое ожидание случайного процесса на выходе стационарной линейной системы, если математическое ожидание СП на входе ЛС известно?
76. Как
найти АКФ случайного процесса на выходе стационарной линейной системы, если АКФ
случайного процесса на входе ЛС известно? Чему она равна, если входной процесс
представляет собой белый шум с АКФ 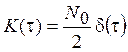 ?
?
77. Как найти спектральную плотность случайного процесса на выходе стационарной линейной системы, если спектральная плотность случайного процесса на входе ЛС известна?
78. Какой
вид имеет спектральная плотность на выходе идеального дифференцирующего звена,
если спектральная плотность входного процесса ![]() ?
?
79. Как
найти корреляционную функцию СП на выходе идеального дифференцирующего звена,
если КФ входного процесса равна ![]() ?
?
80. Как
найти взаимную корреляционную функцию процессов на входе и выходе линейной
системы? Чему она равна, если входной процесс представляет собой белый шум с
АКФ 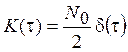 ?
?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.