- оценку остаточной дисперсии
- объясненную дисперсию
- коэффициент детерминации,
если
a) матрица наблюдений ![]()
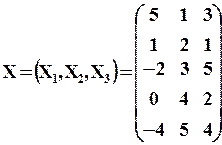
б)![]()
![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() ,.
,. ![]() ,
, ![]()
Задача 1
А) Записать для пар (![]() и
и ![]() ) уравнения регрессии
) уравнения регрессии
1)
в исходной форме (![]() ) и
оценить параметры
) и
оценить параметры
2)
в форме со скрытым свободным членом (![]() ) и оценить параметры
) и оценить параметры
если матрица наблюдений ![]()
![]()

B) Как связаны ![]() и
и ![]() ,
, ![]() и
и ![]() ,
, ![]() и
и ![]()
(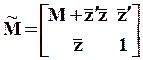 ,
, 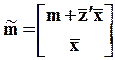 ,
, 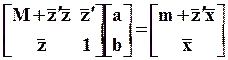 )
)
(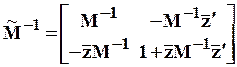 )
)
Задача 2
В регрессии ![]() матрица вторых начальных моментов
регрессоров равна
матрица вторых начальных моментов
регрессоров равна 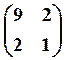 . Найдите дисперсию объясняющей
переменной.
. Найдите дисперсию объясняющей
переменной.
Задача 3
1. Используя
следующие данные ![]()
![]()

а) Построить регрессию ![]() и оценить 95- процентные доверительные
интервалы для параметров регрессии
и оценить 95- процентные доверительные
интервалы для параметров регрессии
б) Проверить значимость коэффициентов регрессии и оценить качества регрессии с вероятностью ошибки 5%
Значения 95-процентные квантилей F- распределений
|
Степень свободы |
Числителя |
||
|
Знаменателя |
1 |
2 |
3 |
|
1 |
161 |
200 |
216 |
|
2 |
18.51 |
19.00 |
19.16 |
|
3 |
10.13 |
9.55 |
9.28 |
|
4 |
7.71 |
6.94 |
6.59 |
|
5 |
6.61 |
5.79 |
5.41 |
Значения 95-процентные квантилейt- распределения
|
Степень Свободы |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Квантили |
12.7 |
4.3 |
3.18 |
2.78 |
2.57 |
2.45 |
2.37 |
2.31 |
Задача 4
Оценка регрессии ![]() на
основе N=30 наблюдений дали следующие результаты:
на
основе N=30 наблюдений дали следующие результаты:
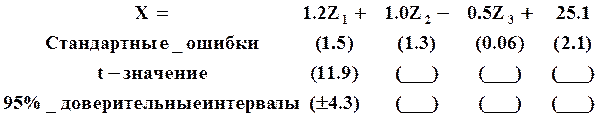
Заполните пропуски.
Взять данные {по номеру в списке + 30*(N) , где N – это последняя цифра номера группы ( 1, 2)}
# первый столбец: X - зависимая переменная
# второй столбец: Z - фактор
Задание сдается в письменном виде с обязательным отражением
всех промежуточных вычислений
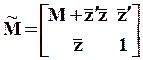 и
и 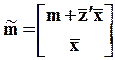 ).
).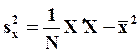 ,
, 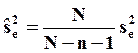 и оцените матрицу ковариации параметров
уравнения регрессии
и оцените матрицу ковариации параметров
уравнения регрессии 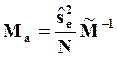
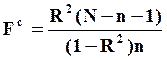 и
используя уровень значимости
и
используя уровень значимости  , вычислите предсказанное значение для
, вычислите предсказанное значение для Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.