Производственные функции с взаимозаменяемыми ресурсами. Показатели использования ресурсов

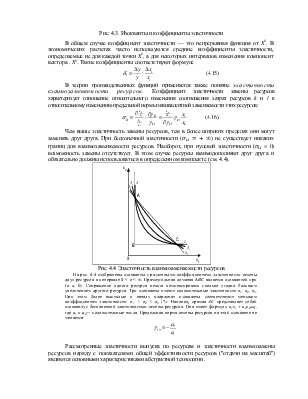
использования ресурсов при неизменном научно-техническом уровне в значительной мере погашают друг друга. Поэтому в пределах краткого времени величина п для народного хозяйства в целом близка единице.

Для однородной функции справедлива формула Эйлера

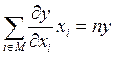                        (4.18)

Разделив обе части этого уравнения на у, получим

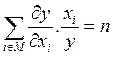                         (4.19)

Выражение 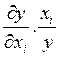 есть коэффициент эластичности δ_i. Поэтому nравно сумме коэффициентов эластичности выпуска по затрачиваемым ресурсам.

Проанализируем подробнее экономический смысл формул (4.18)
и (4.19) при n = 1:    

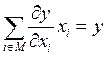                          (4-20)

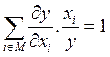                         (4.21)

Поскольку  — это предельная эффективность единицы ресурса i, то 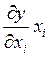 было бы заманчиво интерпретировать как общий объем продукции, произведенной за счет ресурса i.  Весь объем производства у (или единица произведенной продукции) как бы складывается из частей (или разлагается на части), произведенных за счет использования каждого ресурса в отдельности. Выражение (4.21) показывает также, что сумма коэффициентов эластичности однородной производственной функции первой степени равна единице. Из этого в свою очередь следует, что если все коэффициенты эластичности неотрицательны (δ_i ≥ 0), то ни один из них не может быть больше единицы (δ_i ≤ 1).

Изложенные экономические интерпретации выражений (4.20) и (4.21) имеют сугубо условный характер, не вытекающий из технологической природы производственных функций. Нельзя забывать, что на самом деле продукция может создаваться только путем взаимодействия ресурсов. И если какой-либо ресурс s абсолютно необходим для производства (из x_s= 0 следует у = 0), то никакие затраты других ресурсов не могут привести к созданию продукции. Конструктивное значение показателей предельной эффективности заключается не в том, что они определяют роль (вклад) каждого ресурса, а в том, что они позволяют изучать влияние изменения затрат различных ресурсов на изменение объемов производства.

Однако в западной экономической науке интерпретациям формул (4.20) и (4-21) придается исключительно большое значение. Эти формулы используются в теории "трех факторов производства" и теории "вменения" для объяснения процесса создания стоимости (вменение капиталу, труду, земле соответствующих частей стоимости) и теоретического обоснования принципа распределения создаваемой стоимости на заработную плату, прибыль, ренту (в соответствии с предельными продуктами труда, капитала, земли, как основными факторами производства).

Необходимо строго отделять анализ производственных функций как инструмента изучения технико-экономических условий производства от попыток использования производственных функций в теориях образования стоимости и распределения доходов.

Степенная (мультипликативная) производственная функция. Широкое распространение в экономических исследованиях имеет функция вида

                                  (4.22)

Она обладает рядом достоинств: включает небольшое число имеющих явный экономический смысл параметров, имеет производные высших порядков, в большинстве случаев удовлетворительно выравнивает эмпирические данные, весьма удобна для оценки параметров (в частности, благодаря тому, что является линейной относительно логарифмов: . Эта функция включает только безусловно необходимые ресурсы: если какой-либо x_s = 0, то у - 0. Параметр аинтерпретируется как показатель общей эффективности ресурсов (он приводит также в соответствие размерности затрачиваемых ресурсов и производимой продукции).

В соответствии с (4.14), (4.15), (4.16) предельная норма эквивалентной замены ресурсов 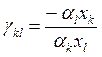 коэффициент эластичности выпуска по i-му ресурсу