Основные понятия экономической динамики. Характеристики экономического развития, страница 3

Таблица 9.2

Между базисными и цепными абсолютными приростами и темпами роста существуют формулы взаимоперехода (см. ДМНХ, с. 11-12).

В качестве количественной иллюстрации введенных понятий рассмотрим данные о росте национального дохода СССР, рассчитанные по табл. 9.1 (см. табл. 9.3).

Таблица 9.3

Характеристики динамики произведенного национального дохода СССР за 1976—1985 гг.

Предельные (непрерывные) абсолютные и относительные приросты. В теоретическом анализе экономической динамики удобно рассматривать время и показатели динамического ряда как непрерывные величины, обладающие в ряде случаев дополнительными свойствами (дифференцируемость и т.д.). Это позволяет применять для характеристики "поведения" траектории аппарат дифференциального исчисления. Соответствующие характеристики скорости и интенсивности будем называть непрерывными.

Непрерывный абсолютный прирост является производной абсолютной величины по времени:

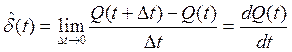                 (9.5)

Непрерывный темп прироста является производной по времени логарифмической функции абсолютного показателя:

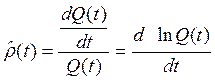          (9.6)

Дополнительной характеристикой скорости развития является абсолютное ускорение

    (9.7)

Оно измеряется как разность между последующим и предшествующим абсолютными приростами. Для непрерывного случая — это вторая производная абсолютной величины по времени:

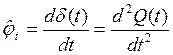                             (9.8)

Средние характеристики развития. Для обобщающей оценки скорости и интенсивности изменения динамического ряда используются средние характеристики. В свою очередь, для исчисления средней каждого показателя применяется множество способов. Эти способы, как правило, ориентированы на решение различных содержательных экономических задач. Наибольшее значение имеют два принципа исчисления средней: 1) исходя из общего абсолютного прироста за период; 2) исходя из суммы абсолютных уровней за период.

Средний абсолютный прирост. Определяющим условием первого, наиболее распространенного способа исчисления данного показателя является величина абсолютного прироста за весь период: