Метод отсечения производственно-транспортной задачи

Метод отсечения производственно-транспортной задачи.

 c_i^rz_i^r + {v_ijb_jk - u_ijA_ij}= П_о +  T_j⁰    →min    

в оптимальном плане =  П_о 

где T_j⁰ – значение функционала  в транспортной задаче при  z_i ^r оптимальном.

 (c_i^r  - a_i^ru_i)z_i ^r £ [П_о + T_j⁰ ] - v_ijb_ij -  ε называется отсечением для многопродуктовой модели

Однопродуктовая модель

Формальная постановка модели

a_i^rz_i^r - y_i ³ 0   "i             z_i^r £ 1                  "i

y_ik ³ b_k                "k           (c_i^rz_i^r + t_iky_ik ) → min

Разобьем эту задачу на две: производственную задачу и транспортную.

Гипотеза:  если эти задачи не имеют решения, то и исходная не имеет решения тоже

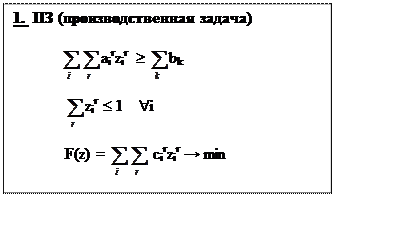
Решая задачу, получаем оптимальное решение z_i^or:  a_i^rz_i^or = A_i^o

Решая задачу, получаем оптимальное решение y_ik^o.

План {z_i^or, y_i^o_k} является не оптимальным, но допустимым в исходной задаче.

Пусть z^o = (z_i^or),  y^o = (y_i^o_k)                 F(z^o) = П_о      Q(y^o) = Т_о

S_о – суммарные затраты:  S_о = П_о + Т_{о =}  c_i^rz_i^r+t_iky_ik 

Составим соотношение:

 c_i^rz_i^r + {b_kv_k - A_iu_i}= S_о     ????

Заменим A_iu_i  на a_i^rz_i^ru_i

Тогда  c_i^rz_i^r -a_i^rz_i^ru_i + b_kv_k £ S_о (т.е. мы потребуем чтобы П1+Т1<S0)

То (c_i^r - a_i^ru_i)z_i^r £ S_о- b_kv_k – ε    (**)  Это есть отсечение, которое отсекает планы, которые с учетом транспортной оценки дает не оптимальный план (транспортные затраты не минимальные).          ПЗ + неравенство (**) = новая задача (решаем на второй итерации)