Межотраслевые модели с внешними связями, страница 3

Потребности в продукции отраслей второй группы полностью удовлетворяются за счет импорта, который получил название "недополняющего" ("неконкурирующего").

С учетом указанных предположений модель межотраслевого баланса производства и распределения продукции объединяет две подсистемы уравнений:

X₁ = A₁₁X₁++V₁ — W₁  (7.26)

A₂₁+X₁+= W₂ (7.27)

Для определения вектора X₁достаточно решить первую систему уравнений (при заданном Y₁= +V₁—W₁), а затем, подставив Х₁ во вторую систему , найти (при заданном W₂) либо W₂(при заданном ).

Применительно к экономике СССР модели (7.24) , (7.25) актуальны прежде всего для регионального звена. Поэтому в дальнейшем будем их анализировать в терминах региональной экономики.

Разбиение отраслей на два подмножества и выделение затрат недополняющего ввоза существенно изменяют экономическое содержание и численные значения региональных коэффициентов полных затрат. Из (7.26), (7.27) следует

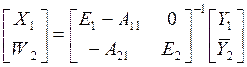            (7.28)

Матрица

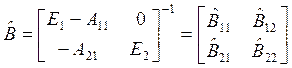
— это матрица коэффициентов полных затрат, характеризующих потребности в продукции, производимой в регионе (первая группа отраслей) и ввозимой из других регионов (вторая группа отраслей), для обеспечения конечных потребностей данного региона. Эти коэффициенты имеют более ограниченную сферу применения по сравнению с коэффициентами полных затрат основного варианта модели. Они правильно определяют полные потребности в продукции собственного производства и внешних ресурсах, но охватывают лишь часть всех затрат народного хозяйства. Так же как и коэффициенты полных затрат основного варианта модели, коэффициенты матрицы могут использоваться для определения полных потребностей в продукции для обеспечения различных фондов конечного продукта. Особый интерес представляют расчеты необходимых объемов _а недополняющего ввоза для обеспечения вывоза продукции  и экономии недополняющего ввоза в результате дополняющего ввоза продукции . По правилам обращения блочных матриц

; ; ;(7.29)

Особенность коэффициентов полных затрат рассматриваемой модификации межотраслевой модели состоит в том, что они совершенно не учитывают затраты на производство продукции второй группы отраслей (в образовании коэффициентов полных материальных затрат не принимают участия блоки А₁₂ и А₂₂). Формулы для и говорят о том, что изменение конечного потребления продукции второй группы отраслей не оказывает влияния на объемы производства продукции первой группы, а только приводит к равному изменению ввоза и объемов продукции второй группы отраслей.

Модель с коэффициентами вывоза и ввоза. Определение значений вывоза и ввоза для отдельного региона встречает значительные трудности, поскольку требует межрегиональных согласований. Для облегчения этой задачи используются гипотезы о пропорциональной зависимости вывоза и ввоза от объемов производства и потребления продукции в регионе:

                            (7.30)

(7.31)

Из (7.31) следует

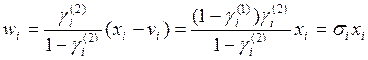
где 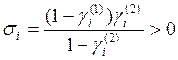 (так как по смыслу <1, <1). Соответственно сальдо вывоза-ввоза определяется как

v_i - w_i= (-σ_i)x_i= q_ix_i                     (7.33)

Очевидно, что эти функции имеют смысл только для продукции, производимой в регионе (iÎJ₁), так как для (iÎJ₂ ) вывоз отсутствует, а ввоз определяется уравнениями (7.29).

С введением (7.33) в систему балансов продукции отраслей подмножества J₁  получаем

(7.34)

или

                  (7.35)

где  — диагональная матрица коэффициентов сальдо вывоза-ввоза, а матрица характеризует полные потребности регионов в выпуске продукции для конечного использования с учетом фиксированных соотношений между производством и межрегиональным обменом.