Линейная регрессия и метод наименьших квадратов (зависимая переменная - потребление электроэнергии в США, количество наблюдений - 437), страница 4

    Сумма квадратов остатков:  6382319.19708573

    Максимум логарифмической функции правдоподобия: -2715.29643468443

    AIC =  12.468175902        BIC =  12.552201987

 

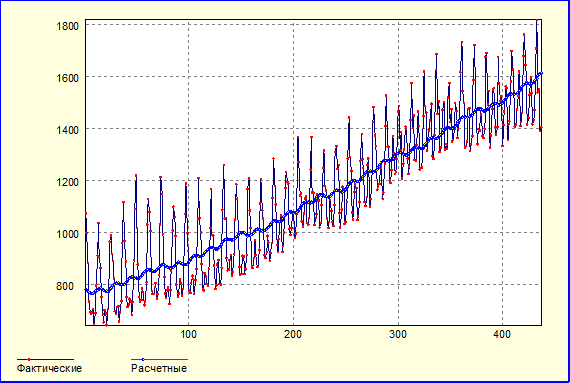
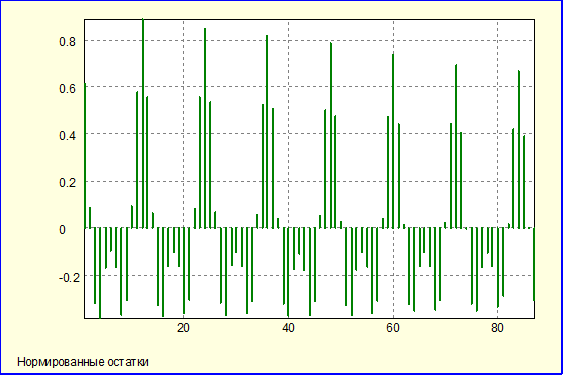
Построенная модель объясняет  более 80% поведения временного ряда. Тем не менее, присутствие очень значительной сезонности процесса ведет к серьезной автокорреляции остатков, которую не удается адекватно смоделировать при помощи сезонных фиктивных переменных.

Таким образом, из всех рассмотренных моделей наилучшим образом поведение временного ряда описывает сглаживание методом скользящего среднего с параметрами m=4, p=3  с последующим моделированием остатков при помощи сезонных фиктивных переменных

A (p,q)

Автокорреляционная функция:

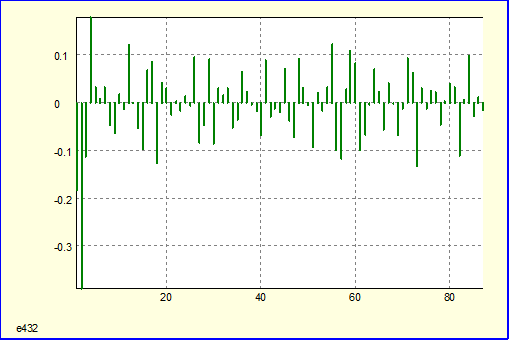
Частная автокорреляционная функция:

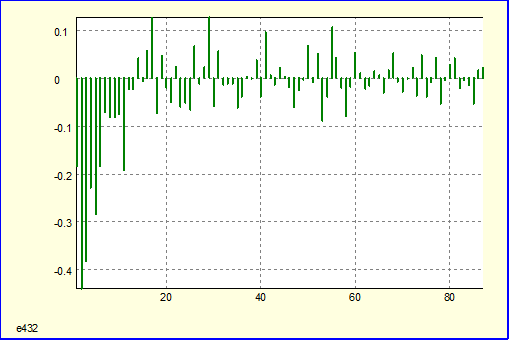
	q	0	1	2	3
p
0			9,02		8,83
1		9,38	9,10
2		9,16	8,53	8,51	8,33
3		8,99	8,67	8,68	8,30
4		8,93	8,59	8,22	8,34
5		8,82	8,46	8,46	8,44
6		8,77
12		8,61

Из всех рассмотренных моделей ARIMA наименьшее значение статистики BIC у ARMA (4,2)

Однако вид частной автокорреляционной функции может свидетельствовать в пользу модели AR (6) (при к=6 наблюдается последнее )

ARIMA (4,2)

   Количество наблюдений: 433

     Переменная           Коэффициент  Станд. ошибка  t-статистика   Знач.  

  1 Константа           -0.0127110482  1.012492E-04  -125.54210839  [0.0000]

  2 %ar1                 0.8931397692  7.72724E-04    1155.8329045  [0.0000]

  3 %ar2                -0.7962295566  3.127951E-04  -2545.5310153  [0.0000]

  4 %ar3                 0.1357309043  1.676195E-05   8097.5612493  [0.0000]

  5 %ar4                 0.0393106505  9.009206E-06   4363.386729   [0.0000]

  6 %ma1                -2.0527829304  5.936654E-16  -3.457811E+15  [0.0000]

  7 %ma2                 1.0532401473  4.082859E-16   2.579664E+15  [0.0000]

    R^2 = 73.513984076%       S.E. = 14.202778298

    Сумма квадратов остатков:  85932.2562521433

    Максимум логарифмической функции правдоподобия: -1759.81026615258

    AIC =  8.1607864487        BIC =  8.2265951418

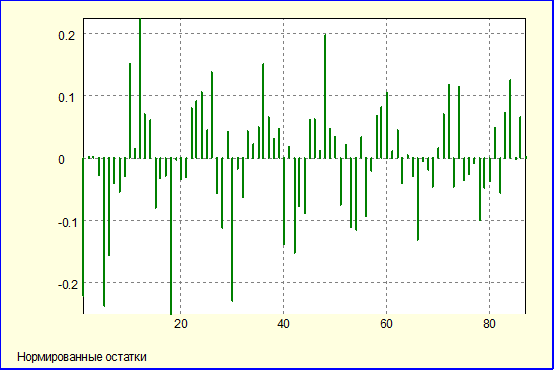
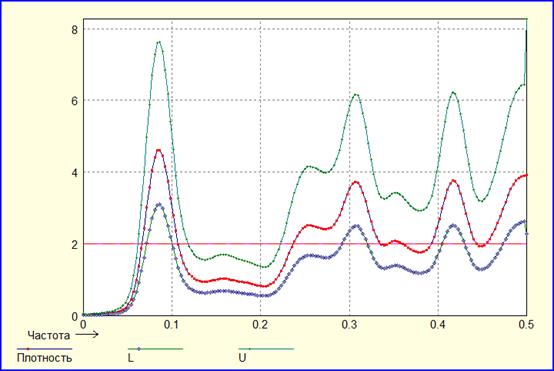
AR (6)

      Количество наблюдений: 431

     Переменная           Коэффициент  Станд. ошибка  t-статистика   Знач.  

  1 Константа            0.0185433907  0.8890708414   0.0208570452  [0.9834]

  2 %ar1                -0.7391663684  0.0437117229  -16.910025941  [0.0000]

  3 %ar2                -1.0138218761  0.0495136991  -20.475583404  [0.0000]

  4 %ar3                -0.9545711269  0.058878541   -16.212547227  [0.0000]

  5 %ar4                -0.6651702063  0.0594047694  -11.197252558  [0.0000]

  6 %ar5                -0.4761283202  0.0501162557  -9.5004767155  [0.0000]

  7 %ar6                -0.2456536493  0.0444499238  -5.5265257667  [0.0000]

    R^2 = 54.587985018%       S.E. = 18.641130528

    Сумма квадратов остатков:  147336.500873723

    Максимум логарифмической функции правдоподобия: -1868.86844140977

    AIC =  8.7047259462        BIC =  8.7707648247

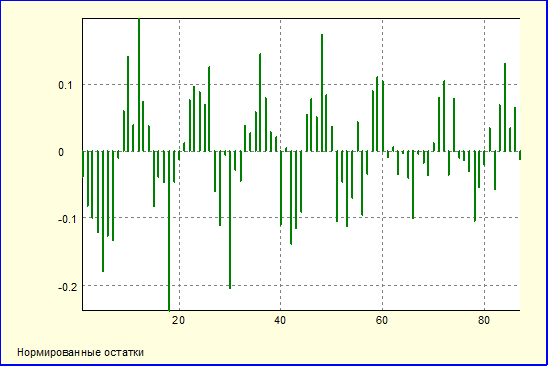
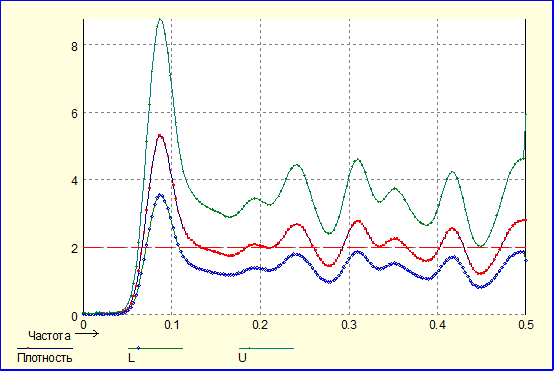
Как видно, при моделировании остатков при помощи моделей ARIMA на мой взгляд не достигается положительного результата (аналогичные результаты получались и при других значениях параметров p и q), в частности вид автокорреляционной функции ухудшается. Как мне кажется в данном конкретном случае можно обойтись без использования моделей ARIMA.