Линейная регрессия и метод наименьших квадратов (зависимая переменная - потребление электроэнергии в США, количество наблюдений - 437), страница 2

  6 март                -0.0653590217  0.0123202206  -5.3050203967  [0.0000]

  7 апр                 -0.2041392732  0.0123202897  -16.569356607  [0.0000]

  8 май                 -0.2263017289  0.0123203989  -18.368052053  [0.0000]

  9 июнь                -0.2041459999  0.012404368   -16.457589717  [0.0000]

 10 июль                -0.1456094829  0.0124041853  -11.738738142  [0.0000]

 11 авг                 -0.1522313327  0.0124040337  -12.272728093  [0.0000]

 12 сент                -0.2461401887  0.0124039141  -19.843751414  [0.0000]

 13 окт                 -0.2279735241  0.0124038276  -18.379288414  [0.0000]

 14 ноя                 -0.1676254818  0.0124037749  -13.514069982  [0.0000]

    R^2adj. = 95.589183938%   DW = 0.5571

    R^2 = 95.720699096%       S.E. = 0.0526246845

    Сумма квадратов остатков:  1.17143819023261

    Максимум логарифмической функции правдоподобия:  673.815524844298

    AIC = -3.0197506858        BIC = -2.8890434438

Все переменные значимы

График остатков:

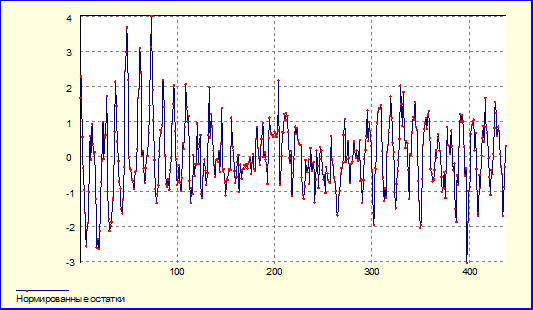
Автокорреляционная функция остатков:

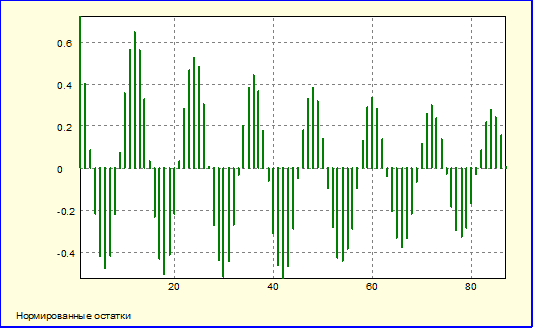
Ситуация аналогичная предыдущему случаю: сильная автокорреляция остатков указывает на их нестационарность, что указывает, что модель недостаточно корректна.

Вид графика временного ряда подсказывает, что следует применить модель с аддитивным ростом и аддитивным сезонным эффектом.

Экспериментально  были подобраны следующие параметры сглаживания:
ag = 0,8;  af = 0,3; ac = 0,01

 Полученный график временного ряда после устранения сезонного эффекта:

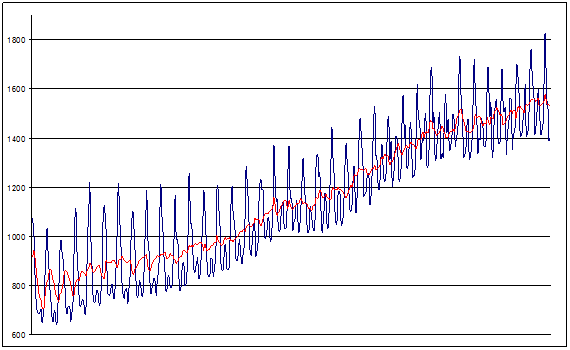
Сглаживание методом скользящей средней

m=3, p=2

График остатков:

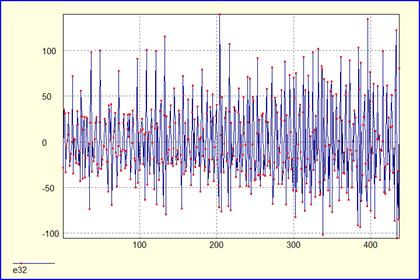
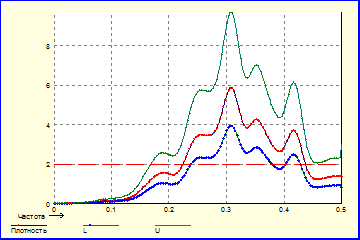
Автокорреляционная функция остатков:

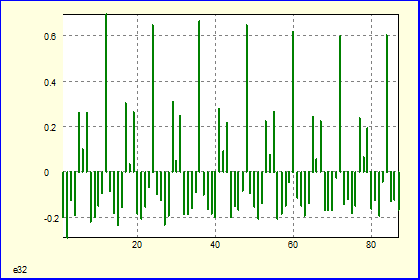
m=4, p=3

График остатков:

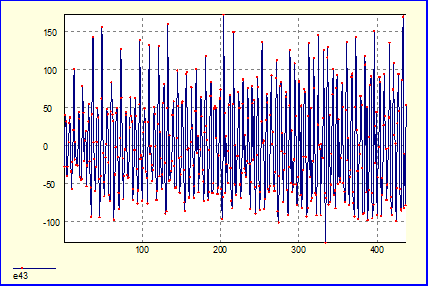
Автокорреляционная функция остатков:

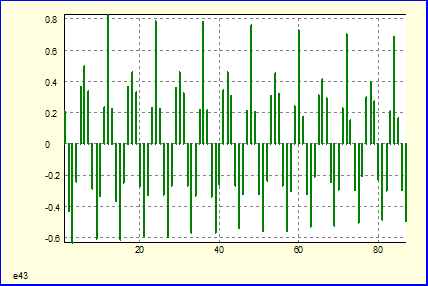
Наблюдается очень значительная автокорреляция остатков, причем при росте задержки k ее значение уменьшается слабо. В обоих случаях попробуем смоделировать данные остатки при помощи фиктивных сезонных переменных:
e32 : 1 $m1 $m2 $m3 $m4 $m5 $m6 $m7 $m8 $m9 $m10 $m11

Переменная           Коэффициент  Станд. ошибка  t-статистика   Знач.  

  1 Константа            38.61164      4.2345124674   9.1183200656  [0.0000]

  2 янв                  26.516388378  5.9479044597   4.4581059696  [0.0000]

  3 фев                 -79.163370811  5.9479044597  -13.309455683  [0.0000]

  4 март                -13.18732      5.9479044597  -2.2171371597  [0.0271]

  5 апр                 -69.988647838  5.9479044597  -11.766942175  [0.0000]

  6 май                 -57.371720811  5.9479044597  -9.6457031547  [0.0000]

  7 июнь                -46.992335833  5.9885049615  -7.8470897387  [0.0000]

  8 июль                -5.5937969444  5.9885049615  -0.9340890557  [0.3508]

  9 авг                 -0.8035002778  5.9885049615  -0.1341737684  [0.8933]

 10 сент                -69.140268611  5.9885049615  -11.545497425  [0.0000]

 11 окт                 -57.559714167  5.9885049615  -9.6117001717  [0.0000]

 12 ноя                 -91.113784722  5.9885049615  -15.214779867  [0.0000]

    R^2adj. = 67.201588074%   DW = 2.6984

    R^2 = 68.029070944%       S.E. = 25.407074805

 

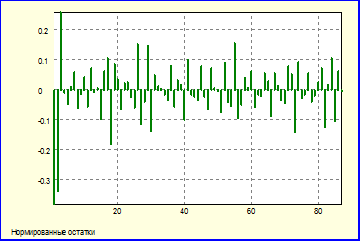
e43 : 1 $m1 $m2 $m3 $m4 $m5 $m6 $m7 $m8 $m9 $m10 $m11

Переменная           Коэффициент  Станд. ошибка  t-статистика   Знач.  

  1 Константа            59.254486111  4.6049410409   12.867588441  [0.0000]

  2 янв                  45.569361727  6.4682179034   7.0451185176  [0.0000]

  3 фев                 -71.519461246  6.4682179034  -11.057058113  [0.0000]

  4 март                -46.21808503   6.4682179034  -7.1454124955  [0.0000]

  5 апр                 -122.04484449  6.4682179034  -18.86838791   [0.0000]

  6 май                 -99.020711517  6.4682179034  -15.308808855  [0.0000]

  7 июнь                -68.102434167  6.512370074   -10.457396216  [0.0000]

  8 июль                 5.6057530556  6.512370074    0.8607853964  [0.3898]