Критерии оптимальности в прикладных моделях, страница 2

Максимизация потребления в заданном ассортименте. Данный подход к оптимизации потребления уже применялся в 8.1. Здесь мы дадим этому подходу более широкую экономическую интерпретацию и проанализируем ряд его модификаций.

Пусть z — количество комплектов (наборов) потребительских благ, а,  — коэффициент, характеризующий количество i-й продукции в комплекте (ассортиментный коэффициент).

Структура потребления продукции выражается условием 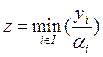, которое соответствует системе линейных неравенств y_i ≥ a_iz, i Î I. Допускается, что при решении задачи на максимум комплектов некоторые виды продукции могут получаться в излишке (сверх комплектов). Такие случаи в оптимизационных задачах возможны при наличии комплексных производств.

Таким образом, задача максимизации потребления в заданном ассортименте включает условия:

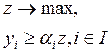                                   (8-14)

Коэффициенты удобно нормировать так, чтобы . Если z— общий объем фонда потребления и , то коэффициенты  означают удельный вес i-й продукции в фонде потребления.

Остановимся на вопросе экономического обоснования ассортиментных коэффициентов.

Широкое применение имеет подход к определению структуры потребления, базирующийся на системе норм рационального потребления продуктов питания, промышленных товаров, жилья, различных услуг. Принимается, что коэффициенты я/ пропорциональны соответствующим нормам рационального потребления. Тогда максимизация потребления в заданном ассортименте будет обозначать равномерное приближение к рациональным нормам. Возникающую задачу можно интерпретировать как максимизацию степени равного удовлетворения рациональных потребностей. Действительно, если  - вектор рациональных потребностей, Ө — степень удовлетворения рациональных потребностей, ӨÎ[0, 1], то имеем

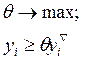(8.15)

Очевидно, что если  где k — коэффициент пропорциональности, k> 0, то условия (8.14) и (8.15) эквивалентны. На рис. 8.1 в точка А соответствует рациональным потребностям. Все наборы благ, удовлетворяющие заданному ассортименту, находятся на луче ОА. Точка В — пересечение луча с границей множества производственных возможностей — является оптимальным решением.

Рис. 8.1

Существенный недостаток условий оптимизации (8.14), (8.15) заключается в том, что допускаются неоправданно резкие изменения сложившейся структуры потребления. Известно, что различные рациональные потребности удовлетворяются в настоящее время не в одинаковой степени (см. табл. 5.1). В этой ситуации мгновенная перестройка фактической структуры потребления на "рациональную" неизбежно должна привести к уменьшению потребления ряда видов благ (например, хлеба, картофеля, сахара), которое не может быть сразу же компенсировано ростом потребления других видов благ (например, мяса, фруктов). Поэтому целесообразно изменить условия оптимизации таким образом, чтобы обеспечить плавность изменения структуры потребления. Для этого следует перейти к задаче максимизации прироста потребления в заданном ассортименте.

Обозначим: — потребление i-и продукции в базисном году;  — прирост потребления продукции iпо сравнению с базисным;  — ассортиментный коэффициент прироста потребления продукции i (удобно, чтобы );  — число комплектов прироста потребления. Тогда условия максимизации формулируются следующим образом:

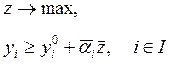                          (8.16)

Соответственно меняется и постановка задачи максимизации степени удовлетворения рациональных потребностей:

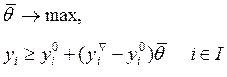                     (8.17)

где— степень удовлетворения потребностей по сравнению с достигнутым уровнем, .

На рис. 8.1а показано, что потребление благ увеличивается от исходной точки Y° прямолинейно в направлении к точке А. При этом структура потребления постепенно приближается к рациональной. Оптимальным решением будет точка D.

Другой подход к определению структуры потребления тесно связан с понятием и свойствами ЦФП (см. 5.1).

Выбранному ассортиментному вектору соответствует, как это видно на рис. 8.1, эффективный (оптимальный по Парето) вариант потребления. Но вовсе не обязательно, что он будет оптимальным с позиций ЦФП. Поиск лучших вариантов может быть продолжен путем изменения ассортиментных коэффициентов.